SOLUTION: You were told that the mean score on a business exam is 68 with the scores normally distributed. In addition, you know the probability of a score between 55 and 60 is 2.5% and that

Something is wrong with this problem.  The two pieces of 
information given are inconsistent.  We only need that
the mean is 68 and P(x > 76) = 0.065 to find the
standard deviation, from which we can easily find  
P(55 < x < 76).  

However using that standard deviation, We get that

P(55 < x < 60) = 0.058, not the 0.025 as is given.   
 
--------------------------------

Here, I'll show this:

So 

Therefore the z-score of x=76

We use a table or use a TI-83 or 84, to find the z-score
such that the area to the right of it is 0.065.  We find 
that as z = 1.51.  That is,

P(z > 1.51) = 0.065

So want to substitute z = 1.51 x = 76 and  in

 to find standard deviation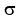 

But first we'll solve that for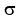 





Now we'll substitute:

That's easy, now that we have the standard deviation .

We find that to be 0.9281

---------------------------

We didn't even need this at all:

However that is inconsistent with .

Because using the standard deviation that we calculated, that

P(55 < z < 60) = 0.058

So the two given pieces of information are inconsistent.

Edwin