SOLUTION: Three six sided dice are thrown and produce a random set of numbers eg 1 4 6 = 11. Now a second set of three six sided dice are thrown. Before we worry about the sum total o

3 dice can fall in exactly 63 or 216 ways.  

3 dice can have sum 3 in exactly 1 way.
3 dice can have sum 4 in exactly 3 ways.
3 dice can have sum 5 in exactly 6 ways.
3 dice can have sum 6 in exactly 10 ways.
3 dice can have sum 7 in exactly 15 ways.
3 dice can have sum 8 in exactly 21 ways.
3 dice can have sum 9 in exactly 25 ways.
3 dice can have sum 10 in exactly 27 ways.
3 dice can have sum 11 in exactly 27 ways.
3 dice can have sum 12 in exactly 25 ways.
3 dice can have sum 13 in exactly 21 ways.
3 dice can have sum 14 in exactly 15 ways.
3 dice can have sum 15 in exactly 10 ways.
3 dice can have sum 16 in exactly 6 ways.
3 dice can have sum 17 in exactly 3 ways.
3 dice can have sum 18 in exactly 1 way.

Note that 1+3+6+10+15+21+25+27+27+25+21+15+10+5+3+1 = 216 = 63.

So there are 216×216 or 46656 ways both sets of dice can fall.
That will be the denominator of the desired probability.

The number of ways both sets of dice can have sum 3 is 1×1 or 1.
The number of ways both sets of dice can have sum 4 is 3×3 or 9.
The number of ways both sets of dice can have sum 5 is 6×6 or 36.
The number of ways both sets of dice can have sum 6 is 10×10 or 100.
The number of ways both sets of dice can have sum 7 is 15×15 or 225.
The number of ways both sets of dice can have sum 8 is 21×21 or 441.
The number of ways both sets of dice can have sum 9 is 25×25 or 625.
The number of ways both sets of dice can have sum 10 is 27×27 or 729.
The number of ways both sets of dice can have sum 11 is 27×27 or 729.
The number of ways both sets of dice can have sum 12 is 25×25 or 625.
The number of ways both sets of dice can have sum 13 is 21×21 or 441.
The number of ways both sets of dice can have sum 14 is 15×15 or 225.
The number of ways both sets of dice can have sum 15 is 10×10 or 100.
The number of ways both sets of dice can have sum 16 is 6×6 or 36.
The number of ways both sets of dice can have sum 17 is 3×3 or 9.
The number of ways both sets of dice can have sum 18 is 1×1 or 1.

1+9+36+100+225+441+625+729+729+625+441+225+100+36+9+1 = 4332

Therefore the desired probability is  =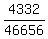 

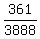or about 0.0928497942

Edwin