SOLUTION: a standard six faced die and a standard four-faced die are both rolled once the cube’s faces are numbered 1-6 and the tetrahedron ‘s faces are numbered 1-4 what is the probability

Here is the sample space, where, for example (4,3) stands for
getting a downward facing 4 on the six-faced die and a downward 
facing 3 on the four-faced die:  

{ (1,1)  (1,2)  (1,3)  (1,4)

  (2,1)  (2,2)  (2,3)  (2,4)

  (3,1)  (3,2)  (3,3)  (3,4)

  (4,1)  (4,2)  (4,3)  (4,4)

  (5,1)  (5,2)  (5,3)  (5,4)

  (6,1)  (6,2)  (6,3)  (6,4)  }

There are 24 outcomes or simple events in the sample space.
I'll color the ones red which have a sum greater than 6

{ (1,1)  (1,2)  (1,3)  (1,4)

  (2,1)  (2,2)  (2,3)  (2,4)

  (3,1)  (3,2)  (3,3)  (3,4)

  (4,1)  (4,2)  (4,3)  (4,4)

  (5,1)  (5,2)  (5,3)  (5,4)

  (6,1)  (6,2)  (6,3)  (6,4)  }

Count the red ones and you'll get that 10 out of the 24 
have a sum greater than 6. So the probability you want is

 which reduces to 

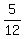Edwin