Question 243421: ok. if i have an eighty percent chance of selecting the right outcome for a particular event, then i know the probability for selecting the right outcome for four, five or six events in a row. but what is the probability of selecting the right outcome four out of six times, or five out of six times. I'm getting a little confused when the outcomes are not in a row. Because four out of six could be four hits in a row or it could be miss,hit,hit,hit,miss,hit and so on. please help. thanks, tim
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! ok. if i have an eighty percent chance of selecting the right outcome for a particular event, then i know the probability for selecting the right outcome for four, five or six events in a row. but what is the probability of selecting the right outcome four out of six times, or five out of six times. I'm getting a little confused when the outcomes are not in a row. Because four out of six could be four hits in a row or it could be miss,hit,hit,hit,miss,hit and so on. please help. thanks, tim
---------------------
Everything you said is correct.
"But what is the probability of selecting the right outcome four out of six times, or five out of six times."
----
Four out of six:
The prob of rrrrww is (0.8)^4(0.2)^2
And prob of rrrwwr is (0.8)^4(0.2)^2
And there are 6C4 = 6C2 = 15 of these patterns.
Each of the patterns has the same probability
and they are all mutually exclusive (that means
if you get one of the patterns you cannot simultaneously
get another one of the patterns).
So you add all those equal probabilities and get
15*0.8^4*0.2^2 = 0.24576....
---------------------------------
Five out of six:
The prob of 5 out of six follows the same logic:
rrrrrw has the same probability as rrrrwr and
there are 6C5=6C1=6 such patterns.
Each pattern has prob = (0.8)^5*(0.2)^1
---
So the prob of 5 out of 6 is 6C5*0.8^5*0.2 = 0.3932...
---------------
In general P(r successes in n trials) = nCr*p^r*q^(n-r)
===========================================================
Cheers,
Stan H.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! ok. if i have an eighty percent chance of selecting the right outcome for a particular event, then i know the probability for selecting the right outcome for four, five or six events in a row. but what is the probability of selecting the right outcome four out of six times, or five out of six times. I'm getting a little confused when the outcomes are not in a row. Because four out of six could be four hits in a row or it could be miss,hit,hit,hit,miss,hit and so on. please help. thanks, tim
You are talking about binomial probabilities.
It doesn't matter whether the right outcomes are in a row or not.
If the probability of 1 success in 1 trial is p, then the probability
of exactly x successes in n trials (regardless of the order in which
the successes occur) is given by this formula:
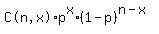 Sometimes
Sometimes 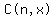 is written is written  and sometimes
it's written and sometimes
it's written 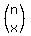 . Sometimes it is called
"n choose x" and sometimes "the combinations of n things
taken x at a time", and sometimes "the n,x binomial coefficient".
But however it's written and whatever
it's called it means . Sometimes it is called
"n choose x" and sometimes "the combinations of n things
taken x at a time", and sometimes "the n,x binomial coefficient".
But however it's written and whatever
it's called it means 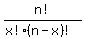 or or
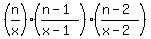  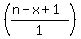 In your problem, the probability of getting exactly 4 successes
out of 6 trials, when the probability of exactly 1 success in 1
trial is .8 can be gotten this way:
n = 6, p = .8, x = 4
In your problem, the probability of getting exactly 4 successes
out of 6 trials, when the probability of exactly 1 success in 1
trial is .8 can be gotten this way:
n = 6, p = .8, x = 4
 In your other problem, the probability of getting exactly 5 successes
out of 6 trials, when the probability of exactly 1 success in 1
trial is .8 can be gotten this way:
n=6, p = .5, x = 5
In your other problem, the probability of getting exactly 5 successes
out of 6 trials, when the probability of exactly 1 success in 1
trial is .8 can be gotten this way:
n=6, p = .5, x = 5
 You can also use a TI-84 calculator to find this
Press CLEAR
Press 2nd
Press VARS
Press ALPHA
Press MATH
You will see this on the screen:
binompdf(
type this 6,.8,4) after it and you will have this on the screen:
binompdf(6,.8,4)
Press ENTER
Read .24576
---------------
For the other one replace the 4 with a 5, and
you'll read .393216
Edwin
You can also use a TI-84 calculator to find this
Press CLEAR
Press 2nd
Press VARS
Press ALPHA
Press MATH
You will see this on the screen:
binompdf(
type this 6,.8,4) after it and you will have this on the screen:
binompdf(6,.8,4)
Press ENTER
Read .24576
---------------
For the other one replace the 4 with a 5, and
you'll read .393216
Edwin
|
|
|