X = no. of aces drawn which can either be 0, 1, 2, or 3.
So make this chart:
 Now we must calculate the probabilities to go in
the bottom row of the chart.
We first calculate the probability of getting 0 aces.
This means we draw 3 non-aces. There are 48 non-aces.
So the number of ways to choose three non-aces is
Now we must calculate the probabilities to go in
the bottom row of the chart.
We first calculate the probability of getting 0 aces.
This means we draw 3 non-aces. There are 48 non-aces.
So the number of ways to choose three non-aces is
 The denominator is
The denominator is  So the probability of getting 0 aces is
So the probability of getting 0 aces is  Next we calculate the probability of getting 1 ace.
This means we draw 2 non-aces and 1 ace. There are
48 non-aces. So the number of ways to choose two
non-aces is
Next we calculate the probability of getting 1 ace.
This means we draw 2 non-aces and 1 ace. There are
48 non-aces. So the number of ways to choose two
non-aces is 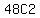 and the number of ways to
choose the ace is
and the number of ways to
choose the ace is 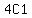 ways. That's
ways. That's
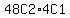 ways.
The denominator again is
ways.
The denominator again is  So the probability of getting exactly 1 ace is
So the probability of getting exactly 1 ace is
 Next we calculate the probability of getting
exactly 2 aces. This means we draw 1 non-ace and
2 ace3. There are 48 non-aces. So the number of
ways to choose one non-aces is
Next we calculate the probability of getting
exactly 2 aces. This means we draw 1 non-ace and
2 ace3. There are 48 non-aces. So the number of
ways to choose one non-aces is 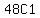 and
the number of ways to choose 2 aces is
and
the number of ways to choose 2 aces is  ways. That's
ways. That's
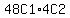 ways.
The denominator is as before
ways.
The denominator is as before  So the probability of getting exactly 2 aces is
So the probability of getting exactly 2 aces is
 Finally we calculate the probability of getting 3 aces.
The number of ways to choose 3 aces is
Finally we calculate the probability of getting 3 aces.
The number of ways to choose 3 aces is  ways.
The denominator is
ways.
The denominator is  So the probability of getting exactly 3 aces is
So the probability of getting exactly 3 aces is
 So we fill in the chart:
So we fill in the chart:
 Now to find the expectation, we add the products of each
value of x times its probability:
Now to find the expectation, we add the products of each
value of x times its probability:
 That rounds to choice C,
That rounds to choice C, 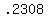 Edwin
Edwin