Question 139000: every 15 min. the fast train arrives & waits 4 min. Then 4 min. after the fast train leaves, the local train arrives & waits 3 min. If you arrive at the station at a random time during the rush period, find the probability that the fast train will be waiting and find the probability that no train will be there.
Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! every 15 min. the fast train arrives & waits 4 min. Then 4 min. after the fast train leaves, the local train arrives & waits 3 min. If you arrive at the station at a random time during the rush period, find the probability that the fast train will be waiting and find the probability that no train will be there.
----------------------------------
Draw the picture of a typical 15 minute period.
fast train: there 4 min; not there 11 min
local train: not there 4; there 3 min ; not there 8 min
----------------------------------
P(fast waiting) = 4/15
P(no train there) = 8/15
=============
Cheers,
Stan H.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! The fast train arrives every 15 minutes and waits 4 minutes. That means that the fast train is there 4 out of every 15 minutes. Pick a random minute out of any 15, and you have 4 possibilities out of 15 that the fast train will be there; probability 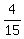
For the second part of the problem. The fast train is at the station for a total of 4 minutes out of 15, and the local is there 3 minutes out of 15. Since there is no overlap, the total time that any train is there is 7 minutes. That means out of every 15 minutes, there are 8 minutes when there is no train there at all. Hence, the probability of having to wait to get on a train is 
|
|
|