SOLUTION: find the probability for rolling a numbered cube. P(rolling a 5, then an even number)

Since the probability of rolling an even number second is not changed,
i.e., neither increased nor decreased in the least by whether or not 
you rolled a 5 first, we say the two events are INDEPENDENT.

So since they are independent, we can multiply their probabilities
to get the probability of both occurring.

P(rolling a 5 first AND rolling an even number second)

= P(rolling a 5 first) x P(rolling an even number second)

A cube has 6 sides, only one of which is numbered 5, but
three of which are numbered with an even number, namely 
2, 4, and 6.

So

P(rolling a 5 first AND rolling an even number second)

= P(rolling a 5 first) x P(rolling an even number second)

= (1 out of 6) x (3 out of 6) = = =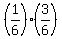 

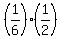Edwin