.
The manufacturing of semiconductor chips produces 2% defective chips. Assume the chips are independent
and that a lot contains 1000 chips. Approximate the probability that between 20 and 30 chips are defective
~~~~~~~~~~~~~~~~~~~~~
This problem is about finding the probability for the binomial distribution.
It has very large number of trials n=1000.
Therefore, using direct formulas for binomial distribution is not recommended: it is a bad style.
Good style is to use a normal distribution as an approximation to the binomial.
This normal distribution has the mean value of m = n*p = 1000*0.02 = 20
and the standard deviation SD = 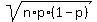 =
=  = 4.42719 (approximate).
Now we should estimate the area under this normal curve between X-score values 20 and 30.
Use your regular calculator TI-83/84 and its standard function normalcdf.
It calculates the cumulative probability for normal distribution.
The pattern to use this function is P = normalcdf ( Xmin, Xmax, mean, SD ).
Xmin Xmax mean SD <<<---=== formatting pattern
Thus the final probability is P = normalcdf ( 19.5, 30.5, 20, 4.42719 ) = 0.5361. ANSWER
Here value 19.5 is the continuity correction factor to Xmin = 20; value 30.5 is the continuity correction factor to Xmax = 30.
For normalcdf, you may also use an online free of charge calculator
https://onlinestatbook.com/2/calculators/normal_dist.html
= 4.42719 (approximate).
Now we should estimate the area under this normal curve between X-score values 20 and 30.
Use your regular calculator TI-83/84 and its standard function normalcdf.
It calculates the cumulative probability for normal distribution.
The pattern to use this function is P = normalcdf ( Xmin, Xmax, mean, SD ).
Xmin Xmax mean SD <<<---=== formatting pattern
Thus the final probability is P = normalcdf ( 19.5, 30.5, 20, 4.42719 ) = 0.5361. ANSWER
Here value 19.5 is the continuity correction factor to Xmin = 20; value 30.5 is the continuity correction factor to Xmax = 30.
For normalcdf, you may also use an online free of charge calculator
https://onlinestatbook.com/2/calculators/normal_dist.html
Solved.