Question 1206113: Assume that 10% of people are left-handed. If we select 10 people at random, find the probability of each outcome below: (Give at least 3 decimal places)
1- There are exactly 5 lefties in the group
2- There are more than 3 lefties in the group
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Assume that 10% of people are left-handed. If we select 10 people at random,
find the probability of each outcome below: (Give at least 3 decimal places)
(1) There are exactly 5 lefties in the group
(2) There are more than 3 lefties in the group
~~~~~~~~~~~~~~~~~~~~~
This problem is a typical binomial distribution.
Use the standard formulas to find probabilities.
The number of trials n= 10; the probability of an individual successful trials p= 0.1.
(1) The number of successful trials k= 5.
P = 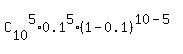 =  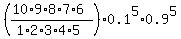= 0.001488 (rounded). ANSWER
You can do it with TECHNOLOGY, using your calculator or Microsoft Excel in your computer or specialized web-site.
If you use MS Excel, you have two options / (two opportunities).
First, you can copy the last formula into MS Excel cell and press the "Enter" button.
You will get the answer P = 0.001488 immediately and momentarily.
Second opportunity is to use Excel-function BINOM.DIST(5, 10, 0.1, FALSE).
Its second parameter is the "number of trials n" (n= 10 in this case);
the first parameter is the "number of successful trials" (k= 5 in this case);
third parameter is "the probability of success in each one single trial" (p= 0.1 in this case); and
the fourth parameter says if you want calculate a single addend or the sum of addends (the single addend in this case).
Input "=BINOM.DIST(5, 10, 0.1, FALSE)" into any MS Excel cell in your computer and press enter to get
the same answer P = 0.001488 immediately.
On Excel function BINOM.DIST, see its description everywhere, for example
https://support.office.com/en-us/article/binom-dist-function-c5ae37b6-f39c-4be2-94c2-509a1480770c
On how to calculate it on TI-83/84 calculators, see
https://www.sayvilleschools.org/site/handlers/filedownload.ashx?moduleinstanceid=3050&dataid=12830&FileName=calc%20directions.pdf
(2) The number of successful trials k >= 4.
P =  .
Use online (free of charge) calculator at this web-site
https://stattrek.com/online-calculator/binomial.aspx
It is very convenient calculator. It provides many options with simple interface.
P(n=10; k >= 4; p=0.1) = 0.01279 (rounded). ANSWER
Solved.
///////////////
If you want to see many similar or different solved problems on binomial distribution probability, look into the lessons
- Simple and simplest probability problems on Binomial distribution
- Typical binomial distribution probability problems
- How to calculate Binomial probabilities with Technology (using MS Excel)
- Solving problems on Binomial distribution with Technology (using MS Excel)
- Solving problems on Binomial distribution with Technology (using online solver)
in this site.
After reading these lessons, you will be able to solve such problems on your own,
which is your PRIMARY MAJOR GOAL visiting this forum (I believe).
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! p = .1
q = 1-p = .9
n = 10
p(x) = p^x * q^(n-x) * c(n,x)
c(n,x) = n! / (x! * (n-x)!)
results are shown below.
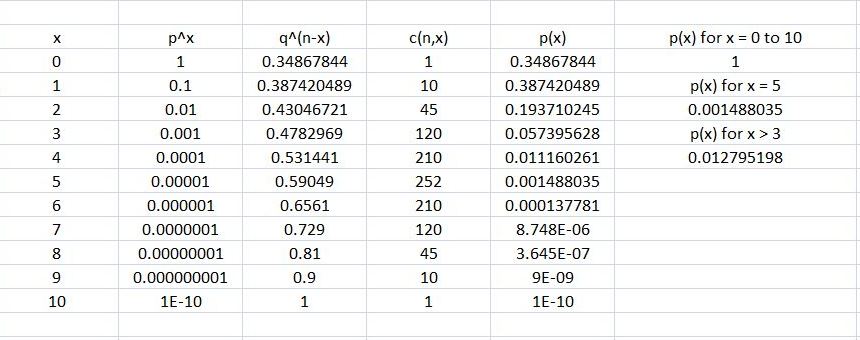
as an example, for x = 5, you get:
p(5) = .1^5 * .9^5 * c(10,5) = .0014880348.
c(10,5) = 10! / (5! * 5!) = (10*9*8*7*6*5!) / (5! * 5!) = (10*9*8*7*6)/(5*4*3*2*1) = 252, as shown for c(10,5) in the spreadsheet.
|
|
|
