Question 1201963: In a certain book, the frequency distribution of the number of words per page may be taken as approximately normal with mean 800 and standard deviation 50. If three pages are chosen at random, what is the probability that none of them has between 830 and 845 words each?
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52810)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a certain book, the frequency distribution of the number of words per page
may be taken as approximately normal with mean 800 and standard deviation 50.
If three pages are chosen at random, what is the probability that none of them
has between 830 and 845 words each?
~~~~~~~~~~~~~~~~~~~~~~~~
Step by step
(1) the probability that in some page the number of words is between 830 and 845 is
P = normalcdf(830, 845, 800, 50) = 0.0902
(using regular calculator TI-83 or TI84 with the standard function normalcdf).
(2) Hence, the probability that in some page the number of words is NOT between 830 and 845 is
the complement to it P' = 1 - 0.0902 = 0.9098.
(3) And finally, the ANSWER to the problem's question is 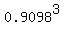 = 0.7531 (rounded). = 0.7531 (rounded).
Solved, with explanations.
//////////////////
In his post, @Theo gives different answer from my number. Why ?
The cause is that @Theo incorrectly treats the problem.
In his solution, he said " since you are looking for the mean of a sample . . . ".
It is the @Theo's error. In this problem, we ARE NOT looking for the mean of a sample.
The problem's question DOES NOT ask about mean of a sample.
It asks about something totally different.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! population mean is 800
population standard deviation is 50
sample size is 3
since you are looking for the mean of a sample, use the standard error rather than the standard deviation.
standard error = standard deviation / sqrt(sample size) = 50 / sqrt(3) = 28.86751346.
probability that the number of words per page in the sample is not between 830 and 845 is equal to .9102
here's what it looks like on a normal distribution calculator.

|
|
|