Question 1201865: The following 7 × 22 grid is divided into squares that are 1 unit by 1 unit.
WebAssign PlotThe shortest possible path on this grid from A to B is 29 units long. One such path is shown in the figure. Let X be the set of all 29-unit-long paths from A to B.
Compute |X|, the number of 29-unit-long paths from A to B.
|X| =
Found 3 solutions by mananth, ikleyn, greenestamps:
Answer by mananth(16946)   (Show Source): (Show Source):
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The following 7 × 22 grid is divided into squares that are 1 unit by 1 unit.
The shortest possible path on this grid from A to B is 29 units long.
One such path is shown in the figure. Let X be the set of all 29-unit-long paths from A to B.
Compute |X|, the number of 29-unit-long paths from A to B.
~~~~~~~~~~~~~~~~~~~~~~
Indeed, the figure is not shown, and it can perplex a reader.
But notice that 29 = 7 + 22, and it makes the meaning of the problem UNIQUE even without a plotted figure.
The points A and B are opposite vertices of the 7x22 rectangle
and the shown path is a path on the grid, comprised of vertical and horizontal segments
of the grid from corner A to corner B, such that a path represents
a piece-wide monotonic function.
For better understanding, this grid has 7 segments in one direction and 22 segments in other direction;
but the number of the vertices of the grid is (7+1) = 8 in one direction and (22+1) = 23 in the other direction.
We can think that 22 segments of the grid are horizontal and 7 segments are vertical,
and A is the left lowest corner of the grid, while B is the upper right corner.
So, we can think that the associated function is a piece-wide monotonically increasing.
The meaning of the problems remains the same at any other disposition of the grid
and the corners A and B.
Notice that vertical increments of the function are not necessary one vertical segment
of the grid: it can be two segments or three etc., but the governing rule is that the
associated function is a piece-wide MONOTONIC - it provides the shortest path.
Then it becomes CLEAR that this problem is the same as to ask,
in how many ways 22 (undistinguishable) objects can be distributed (placed) in 8
distinguishable boxes in a way that the empty boxes are allowed.
In other words, it can be re-formulated in this way: how many solutions this equation
 + +  + +  + +  + + 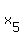 + + 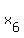 + + 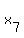 + + 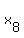 = 22 (1) = 22 (1)
may have in integer non-negative numbers  , i = 1, 2, 3, . . . , 8. , i = 1, 2, 3, . . . , 8.
In this form, it is a typical problem to be solved by the "stars-and-bars" method.
About this method, see this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_%28combinatorics%29
or my lesson
- Stars and bars method for Combinatorics problems
in this site.
The answer is THIS: the number of solutions to equation (1) is
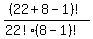 = = 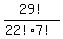 = = 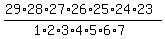 = 1560780.
ANSWER. The number of paths in this problem is 1560780. = 1560780.
ANSWER. The number of paths in this problem is 1560780.
Solved.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The figure is described as a 7x22 grid of unit squares, so we don't need to see the figure....
Assuming this is a problem where A and B are opposite corners of the grid, the number of paths of length 29 from A to B is

To understand the reason for that answer, let B be 22 units to the right of A and 7 units above A. Then any path from A to B of length 29 has to move 22 "steps" to the right ("R") and 7 steps up ("U").
So each path of length 29 from A to B consists of some arrangement of the symbols
RRRRRRRRRRRRRRRRRRRRRRUUUUUUU
By a well-known counting principle, the number of ways to do that is the number shown above.
ANSWER: 
|
|
|