Question 1195519: In the 6/49 lotto game, suppose that the minimum prize is 20 pesos, which you can win by guessing 3 out of 6 numbers correctly. The prize goes up as you guess more numbers correctly. What is the probability of not winning prizes of any amount?
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In the 6/49 lotto game, suppose that the minimum prize is 20 pesos,
which you can win by guessing 3 out of 6 numbers correctly.
The prize goes up as you guess more numbers correctly.
What is the probability of not winning prizes of any amount?
~~~~~~~~~~~~~~~~~~~~~
Surely, such problem should start with clear formal description of this
lotto game - - - but this one does not.
Therefore, I will give my own description, as I understand the problem.
Six numbers are drawn from a set of 49 different numbers 1,2,3,...,49.
If a ticket matches at least three numbers, the ticket wins.
The prize goes up as you guess more numbers correctly.
What is the probability of not winning prizes of any amount?
Solution
First, let's calculate the number of all issued/(possibly existing) tickets.
The total number of all issued/(possibly existing) tickets is the number
of combinations of 49 items taken 6 at a time. It is the number of combinations
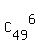 = =  = 13983816.
Favorable (winning) tickets are those that carry at least 3 of 6 different drawn numbers.
In accordance to it, UNWINNING tickets are those that
- (a) carry zero of 6 drawn numbers;
- (b) carry only one of 6 drawn numbers;
- (c) carry only two of 6 drawn numbers.
So, we divide 49 numbers in two categories: 6 selected (drawn) numbers and the rest 49-6 = 43 numbers.
In category (a), we have = 13983816.
Favorable (winning) tickets are those that carry at least 3 of 6 different drawn numbers.
In accordance to it, UNWINNING tickets are those that
- (a) carry zero of 6 drawn numbers;
- (b) carry only one of 6 drawn numbers;
- (c) carry only two of 6 drawn numbers.
So, we divide 49 numbers in two categories: 6 selected (drawn) numbers and the rest 49-6 = 43 numbers.
In category (a), we have  tickets;
In category (b), we have tickets;
In category (b), we have 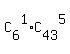 tickets;
In category (c), we have tickets;
In category (c), we have 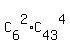 tickets.
+---------------------------------------------------------------------+
| Notice that the order of numbers in tickets does not matter - |
| - therefore we use combinations. |
+---------------------------------------------------------------------+
These three categories are DISJOINT - - - therefore, the total of UNWINNING tickets is the sum tickets.
+---------------------------------------------------------------------+
| Notice that the order of numbers in tickets does not matter - |
| - therefore we use combinations. |
+---------------------------------------------------------------------+
These three categories are DISJOINT - - - therefore, the total of UNWINNING tickets is the sum
 + + 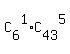 + + 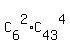 = 6096454 + 6*962598 + 15*123410 = 13723192.
Now the last step to find the probability of getting unwinning ticket is this fraction
P = = 6096454 + 6*962598 + 15*123410 = 13723192.
Now the last step to find the probability of getting unwinning ticket is this fraction
P = 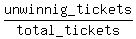 = = 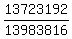 = 0.981362455.
ANSWER. The probability of getting unwinning ticket is 0.98126 (rounded). = 0.981362455.
ANSWER. The probability of getting unwinning ticket is 0.98126 (rounded).
Solved.
It is a good problem of an advanced level.
|
|
|