Question 1188940: A big cube of 10 inch, painted throughout, cut into 103
small cubes each of
one inch. One cube is drawn at random from the collection of thousand cubes. What
is the probability that the cube drawn has, (i) exactly one side painted (ii) exactly
two sides painted, (iii) exactly three sides painted, and (iv) either of the (i), (ii) and
(iii)?
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A big cube of 10 inch, painted throughout, cut into  small cubes each of one inch. small cubes each of one inch.
One cube is drawn at random from the collection of thousand cubes.
What is the probability that the cube drawn has,
(a) exactly one side painted
(b) exactly two sides painted,
(c) exactly three sides painted, and
(d) either of the (a), (b) and (c) ?
~~~~~~~~~~~~~~~~~~~
The number of exterior cubes is  - - 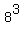 = 1000 - 512 = 488.
Of them, 8 cubes are exactly three-sides painted (at the corners);
8*12 = 96 cubes are exactly two-sides painted (along the 12 edges, but not the corner cubes);
and the rest cubes, 488 - 8 - 96 = 384 = = 1000 - 512 = 488.
Of them, 8 cubes are exactly three-sides painted (at the corners);
8*12 = 96 cubes are exactly two-sides painted (along the 12 edges, but not the corner cubes);
and the rest cubes, 488 - 8 - 96 = 384 =  = 6*64 are one-side painted.
THEREFORE,
(a) P = = 6*64 are one-side painted.
THEREFORE,
(a) P = 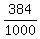 = 0.384;
(b) P = = 0.384;
(b) P = 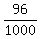 = 0.096;
(c) P = = 0.096;
(c) P = 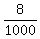 = 0.008;
(d) P = = 0.008;
(d) P = 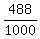 = 0.488. = 0.488.
Solved, answered and carefully/thoroughly/comprehensively explained.
|
|
|