Question 118734: A coin is tossed three times. Use this information to solve these problems.
1.) List the sample space.
2.) Find the probability of tossing heads exactly twice.
3.) Find the probability of tossing tails at least twice.
Any help would be great! Thanks
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! Let H represent an outcome of heads and T represent an outcome of Tails
.
For three tosses of the coin all the possible outcomes are:
.
H-H-H
T-H-H
H-T-H
H-H-T
T-H-T
T-T-H
H-T-T
T-T-T
.
These eight possible outcomes are the sample space.
.
To find the probability of tossing heads exactly twice look down the sample space list and
find any outcome that has exactly two H's. The possibilities are T-H-H, H-T-H, and H-H-T.
This means that three of the eight possible outcomes contain exactly two heads. Therefore,
the probability of throwing exactly two heads in three tosses of the coin is 3 out of 8,
or  or the decimal equivalent of which is 0.375 or 37.5 percent.
.
The probability of tossing tails at least twice can be found by looking down the list of eight
possible outcomes and finding each outcome that has two or more tails in it. The outcomes that
have at least two tails in them are T-H-T, T-T-H, H-T-T, and T-T-T. Therefore, there are
four of the eight outcomes that have two or more tails in them. This means that the probability
of throwing at least two tails in three tosses is 4 out of 8, which is  which reduces
to  and this is 0.50 or 50 percent.
.
Hope this helps you to understand the problem a little better. Note that for each toss
of a coin there are only two possible outcomes, heads or tails. In three tosses the number
of possible outcomes is  which equals the eight possible answers that we found.
If the sample space consisted of tossing the coin 4 times the number of possible outcomes
would be 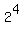 or 16 possible combinations in the sample space.
.
One way to view the sample space is to raise the number of possible outcomes on each trial
to the power of the number of trials. Suppose you roll a die twice (the same as rolling
a pair of dice once). Each die has 6 possible outcomes (the numbers 1, 2, 3, 4, 5, and 6).
And if you roll the die twice you have  or 36 possible outcomes. Try it as an exercise
starting with 1&1, 1&2, 1&3, 1&4, 1&5, 1&6, 2&1, 2&2, 2&3, 2&4, and so on until you get
to the last possible combination of 6&6. If you count up all the possible combinations,
you will find 36 possible outcomes.
.
|
|
|
