Question 1183858: 4. A box contains 5 red balls, 3 white balls and 2 green balls. Two balls will be taken at random, without replacement, and the colors noted (in order).
(a) If the first ball is red, what is the (conditional) probability that the second ball is also red? (You don’t need a formula for this)
(b) Draw the tree diagram for this experiment - show the probabilities on the branches (as in the model).
(c) What is the probability of getting two red balls?
(d) What is the probability of getting exactly one red ball?
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A box contains 5 red balls, 3 white balls and 2 green balls. Two balls will be taken at random, without replacement,
and the colors noted (in order).
(a) If the first ball is red, what is the (conditional) probability that the second ball is also red?
(You don’t need a formula for this)
(b) Draw the tree diagram for this experiment - show the probabilities on the branches (as in the model).
(c) What is the probability of getting two red balls?
(d) What is the probability of getting exactly one red ball?
~~~~~~~~~~~~~~~~~~~~
(a) If the 1st ball is red, then at the 2nd draw you select red ball from remaining 4 red balls among remaining 4+3+2 = 9 balls,
so the probability to draw a red ball at the 2nd draw is  . ANSWER
(it is, actually, the conditional probability, calculated in the reduced space of events.).
(b) I miss this part <<<---=== due to my firm belief, it is NON-neccessary in this problem.
(c) P = . ANSWER
(it is, actually, the conditional probability, calculated in the reduced space of events.).
(b) I miss this part <<<---=== due to my firm belief, it is NON-neccessary in this problem.
(c) P =  = = 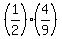 = =  . ANSWER
In the formula, the first factor is the probability to get red ball at the first draw;
the second factor is the probability to get red ball at the 2nd draw.
The formula is SELF-EXPLANATORY.
(d) The number of all (unordered) pairs is . ANSWER
In the formula, the first factor is the probability to get red ball at the first draw;
the second factor is the probability to get red ball at the 2nd draw.
The formula is SELF-EXPLANATORY.
(d) The number of all (unordered) pairs is  = =  = 5*9 = 45. It is the total space of events.
The number of all favorable (preferable) pairs is 5*(3+2) = 5*5 = 25 (one red and one other-color ball in each pair).
THEREFORE, the probability in this case is = 5*9 = 45. It is the total space of events.
The number of all favorable (preferable) pairs is 5*(3+2) = 5*5 = 25 (one red and one other-color ball in each pair).
THEREFORE, the probability in this case is  = = 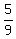 . ANSWER . ANSWER
Solved, answered and thoroughly explained.
|
|
|