SOLUTION: Suppose the probability of snow is 20%, and the probability of a traffic accident is 10%. Suppose further that the conditional probability of an accident, given that it snows, is 4

This problem relates, as you may conclude from the text, to conditional probability.


Let A be the event of snow.              Its probability is  20% = 0.2  (given).    (1)

Let B be the event of traffic accident.  Its probability is  10% = 0.1  (given).    (2)


The event of an accident, given that it snows, is the conditional probability  P(B|A).


This conditional probability  P(B|A)  is the ratio  P(B|A) = P(A ∩ B) / P(A).


Its value is given by the condition : it is  P(B|A) = 40% = 0.4.  So,  P(A ∩ B) / P(A) = 0.4.    (3)



Having  known (3) and (1), you can calculate  P(A ∩ B) = 0.4 * P(A) = 0.4 * 0.2 = 0.08.



        It is the key step in the solution:  from the given data we managed to determine that  P(A ∩ B) = 0.08.

        At this point, make a deep breath, and we will go further.



The problem asks us about OTHER conditional probability  P(B|A)  of the event  "snows, given that there is an accident".


This conditional probability is the ratio  P(B|A) = P(A ∩ B) / P(B).


We just know  P(A ∩ B), which is 0.08 (see (4) ). And we know P(B) = 0.1 (given)  (see (2) ).


THEREFORE,  P(B|A) = P(A ∩ B) / P(B) = 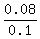 = 0.8.


The problem is just solved and you get the


ANSWER.  The conditional probability that it snows, given that there is an accident, is 0.8.