SOLUTION: Estimate the minimum sample size needed to achieve the margin of error Eequals 0.006 for a​ 95% confidence interval. The minimum sample size is

The other person's answer is WRONG, as in MOST cases! 
Even if he did calculate the ESTIMATED SIZE correctly, he doesn't seem to know that when ROUNDING off, in cases such as this one, ONE needs
to ROUND UP, not DOWN!! Does a person who attempts to help people with math problems need to be told this? He/She shouldn't but obviously he needs to!

Before getting to the correct answer, you need to know - if you don't already - that the ESTIMATED MINIMUM SAMPLE PROPORTION/SIZE
should be calculated using the following formula: n = p̂q̂, where:    
                                                                            = Estimated Minimum Sample Proportion/Size (Unknown, in this case)
                                                                            p̂ = Preliminary Estimate (.5, in this case: see below)                    
                                                                            q̂ = 1 - p̂ (also .5, in this case: see below)
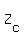                                                                            =  point, based on a 95% confidence interval (1.96, in this case: see below)
                                                                            = Margin of Error (.006, in this case)

Now, since NO PRELIMINARY ESTIMATE, or p̂ WAS GIVEN/AVAILABLE, then .5(50%) should be used for p̂, or for the ASSUMED proportion
With p̂ being .5, q̂ = 1 - p̂ = 1 - .5 = .5
Since this is a 95% CONFIDENCE INTERVAL, then significance level is , and so, 

Estimated Minimum Sample Proportion/Size, or n = p̂q̂ now becomes: 

You can also use STATDISK, any other statistical software, or online calculator to calculate this.
If you do, you should get the same result: 26,678 objects.