Question 1153955: GreenBeam Ltd. claims that its compact fluorescent bulbs average no more than 3.55 mg of mercury. A sample of 40 bulbs shows a mean of 3.62 mg of mercury. The standard deviation is 0.23mg and I found the test statistic which is 1.92 but I need help Finding the p-value. (Round intermediate calculations to 2 decimal places. Round your answer to 4 decimal places.) I don't understand how to do it in excel.
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website!
You have the correct z test statistic. Nice work so far.
Now you'll use the NORM.DIST function in excel. More info can be found here
The general template of the function is
=NORM.DIST(x, mean, standard_dev, cumulative)
In your case, you will type in
=NORM.DIST(1.92, 0, 1, 1)
The x is the z score you got
the mean and standard deviation are 0 and 1 respectively
Cumulative is set to 1 to indicate we want the area under the normal curve. You can use "TRUE" in place of "1" for the cumulative part. So your command could look like this: =NORM.DIST(1.92, 0, 1, TRUE)
The result of that excel calculation is approximately 0.97257105
This is the area under the curve to the left of z = 1.92
Subtract this from 1 (see note below) to get
1-0.97257105 = 0.02742895
which is also approximate
This is the approximate area under the standard normal curve that is to the right of z = 1.92
The p value is approximately 0.0274
Note: the reason why I knew to subtract from 1 is because of the hypothesis. The null hypothesis is  (which is where the claim is being made) and the alternative hypothesis is 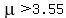 which runs counter or opposite to the claim made in the null. The alternative hypothesis tells us we have a right tailed test.
|
|
|
