.
The first sentence means that repetitions are allowed in the code's digits.
The possible values for the random variable X are {0, 1, 2, 3, 4, 5}.
X= 0 means that there is NO zero among five digits of the code.
The probability do not have zero in any one fixed/selected of 5 positions is 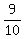 ;
The provability do not have zero in ALL 5 positions, is, therefore,
;
The provability do not have zero in ALL 5 positions, is, therefore, 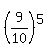 .
X= 1 means that there is exactly one 0 among five digits of the code.
The probability for it is
.
X= 1 means that there is exactly one 0 among five digits of the code.
The probability for it is 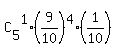 =
= 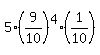 .
X= 2 means that there is exactly two 0 among five digits of the code.
The probability for it is
.
X= 2 means that there is exactly two 0 among five digits of the code.
The probability for it is 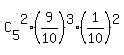 .
The pattern is just clear. The probability for X = k, where k= 0, 1, 2, 3, 4, 5, is
.
The pattern is just clear. The probability for X = k, where k= 0, 1, 2, 3, 4, 5, is
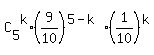 .
.
Solved.
-------------
CHECK. You may check that the sum of these 6 partial probabilities is 1.
Indeed, this sum is equal to 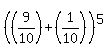 =
= 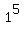 = 1.
= 1.