Question 1111064: How many positive integers between 200 and 500 are divisible by each of the integers 4, 6, 10 and 12? Please give a detailed explanation with each tiny step explained a lot.
Thank you for helping.
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! According to my calculator,
500 is not divisible by 12.
500 divided by 12 is 41.6666.....
That means that 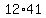 is is
the largest multiple of 12 that is not more than 500,
or (in other words)
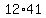 is the largest integer between 1 and 500 that is divisible by 12. is the largest integer between 1 and 500 that is divisible by 12.
What about 200?
200 is not divisible by 12.
200 divided by 12 is 16.6666.....
That means that 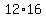 is is
the largest integer between 1 and 200 that is divisible by 12.
All integers between 1 and 500 are positive integers, of course,
but how many of them are between 200 and 500?
Well, there are  positive integers between 1 and 500: positive integers between 1 and 500:
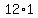 , ,  , , 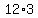 , ....... , , ....... , 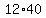 , and , and 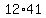 . .
However, the first  of those, from of those, from 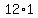 to to 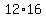 , are less than 200, , are less than 200,
so the number of integers between 200 and 500 are divisible by 12 is
 . .
How did we get that number?
We divided 500 by 12 and 200 by 12,
and we calculated the difference between the integer quotients
not considering remainders.
If using a calculator, we just used the integer part of the result.
The number of integers between 200 and 500 that are divisible by 6 is
 , ,
because 200 divided by 6 is 33.33333.... (or 33, remainder=2),
and 500 by 6 is 83.33333.... (or 83, remainder=2).
The case with integers divisible by 4 is trickier.
 is divisible by 4, and so is is divisible by 4, and so is  . .
Do they count as "between 200 and 500"?
If they count, we have to count the first  multiples of 4, multiples of 4,
but subtract the first 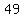 to get to get  . .
If neither 200 nor 500 is considered to be "between 200 and 500",
then there are  less, less,  numbers divisible by 4 numbers divisible by 4
between 200 and 500, not counting 200 or 500.
Similarly, the numbers between 200 and 500 that are divisible by 
are  if we count if we count  and and  , but they are , but they are  if we do not count either 200 or 500. if we do not count either 200 or 500.
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will consider integer numbers from 201 to 500 INCLUSIVELY.
The number of such integer numbers is 500-200 = 300. (It is VERY good number,
since it is divisible by any of 4, 6, 10, 12, 20, 30, 50, 60 . . . )
Of these 300 numbers,
there are 300/4 = 75 numbers divisible by 4. Let me denote this set of numbers as Z4.
300/6 = 50 numbers divisible by 6. Let me denote this set of numbers as Z6.
300/10 = 30 numbers divisible by 10. Let me denote this set of numbers as Z10.
300/12 = 25 numbers divisible by 12. Let me denote this set of numbers as Z12.
Now I need to find the number of elements in the union set Z4 U Z6 U Z10 U Z12.
I can easily simplify my task by noticing that Z12 is just included into Z4 U Z6 (as their intersection !).
So, all I need is to find the number of elements in the union set Z4 U Z6 U Z10.
Now I will use THIS STATEMENT:
If A, B and C are finite sub-sets of the universal set U, then
|A U B U C| = |A| + |B| + |C| - |A n B| - |A n C| - |B n C| + |A n B n C|. (*)
Here |X| denotes the number of elements in a finite subset X. (And the symbol "n" denotes the intersection of sub-sets).
I will not prove this statement here (although it is absolutely elementary).
I will refer you to my lessons in this site
Counting elements in sub-sets of a given finite set
Advanced problems on counting elements in sub-sets of a given finite set
instead.
Now, from the formula (*)
|Z4 U Z6 U Z10| = |Z4| + |Z6| + |Z10| - |Z4 n Z6| - |Z4 n Z10| - |Z6 n Z10| + |Z4 n Z6 n Z10|. (**)
Here |Z4|, |Z6| and |Z10| are just known to you numbers 75, 50 and 30.
|Z4 n Z6| is the number of those integers from 201 to 500 that are divisible by 12; this number is 300/12 = 25.
|Z4 n Z10| is the number of those integers from 201 to 500 that are divisible by 20; this number is 300/20 = 15.
|Z6 n Z10| is the number of those integers from 201 to 500 that are divisible by 30; this number is 300/30 = 10.
Finally, |Z4 n Z6 n Z10| is the number of those integers from 201 to 500 that are divisible by 60; this number is 300/60 = 5.
Therefore, the formula (**) becomes
|Z4 U Z6 U Z10| = 75 + 50 + 30 - 25 - 15 - 10 + 5 = 110.
Thus the number of those integer between 201 and 500 that are divisible by 4, 6, 10 and 12 is 110.
******************************
*** The problem is SOLVED. ***
******************************
|
|
|