Question 1078362: An urn contains
7
white and
6
green balls. Four balls are randomly drawn from the urn in succession, with replacement. That is, after each draw, the selected ball is returned to the urn. What is the probability that all
4
balls drawn from the urn are white?
Found 3 solutions by dkppathak, natolino_2017, MathTherapy:
Answer by dkppathak(439)   (Show Source): (Show Source):
You can put this solution on YOUR website! An urn contains
7
white and
6
green balls. Four balls are randomly drawn from the urn in succession, with replacement. That is, after each draw, the selected ball is returned to the urn. What is the probability that all
4
balls drawn from the urn are white?
solution
total balls are=13
probability of white ball =7/13
balls are replaced and 4 ball are drawn with replacement every time probability of white ball will be =7/13
probability of all 4 balls are white =7/13x7/13x7/13x7/13=7x7x7x7/13x13x13x13
=2401/28561
Answer by natolino_2017(77)   (Show Source): (Show Source):
You can put this solution on YOUR website! P()=P(Pick a white ball)*P(Pick a white ball)*P(Pick a white ball)*P(Pick a white ball).
P(Pick a white ball)= 7/(6+7)=7/13.
P()=(7/13)^4 = 2401/28561 = 0.0841 = 8.41%
*******bonus: if the question switches to without replacement:
P() =P(pick a white ball)* P(pick another white ball) *P(pick another white ball(2)) * P(pick another white ball(3)).
P()= 7/(6+7) * 6/(6+6)* 5/(6+5)* 4/(6+4) = 7/143 = 0.0196 = 1.96%*************
#natolino
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! An urn contains
7
white and
6
green balls. Four balls are randomly drawn from the urn in succession, with replacement. That is, after each draw, the selected ball is returned to the urn. What is the probability that all
4
balls drawn from the urn are white?
Probability that one ball drawn will be white: 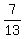
Probability that FOUR balls drawn, after replacing each ball that's drawn, will be white: 
Note to one of the persons who responded:
7 * 7 * 7 * 7/13 * 13 * 13 * 13 DOES NOT equal 0.084065684. That equals 405,769, which means that your answer is WRONG.
|
|
|