Question 1058778: 12 samples of x.
Where
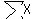 = 2460 = 2460
therefore mean = 2460/12 = 205
also,
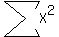 = 504476 = 504476
therefore variance = 
and therefore standard deviation = 4
"A) Test hypothesis that the mean of the probability distribution of X is not significantly different from 208"
"B) Test hypothesis that the standard deviation is not significantly different from 3.0"
in both cases, 
Which, on the T-table, with 11 degrees of freedom, gives a value of 3.106. But not sure how to put that into practice, any help is greatly appreciated.
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! Testing the sd as being the same as sigma is a chi-square test with 11 degrees of freedom (n-1) and has a value of (n-1)s1^2/sigma^2
That value is 11(16)/9=176/9=19.56
That has a probability of 0.0519. At the 0.05 level, the sd is not significantly different from the population sd.
Therefore, the assumption of the sample variance being equal to the population variance is valid (although barely, it still meets the criteria).
If the sample mean were 205, then t=(205-208)/s/ sqrt(n)=-3(sqrt(12))/4=-2.60.
The t-value of 3.106 obtained is checked against the t-value with 11 df and t(0.995), or the 1% level, not the 5% level. The critical value is > 2.201 or less than -2.201 You use the 0.975 value for a 2 tailed test when alpha is 0.05, because half the alpha is on one side of the curve and half on the other.
The value of t calculated is -2.60, which is less than -2.201. Therefore, at the 5% level, the mean calculated is significantly different from the postulated mean of 208.
|
|
|