SOLUTION: A and B are two independent events. The probability that both occur simultaneously is 1/6 and the probability that neither occurs is 1/3, then P(A) + P(B) = *? A. 2/3 B. 4/7

Therefore the probability that they both occur simultaneously
is the product of their respective probabilities.

P(A and B) = P(A)*P(B)

P(A)*P(B) = 1/6

Since A and B are independent, then so are A' and B',
the events that they do not occur.  
P(A') = 1-P(A)
P(B') = 1-P(B)

P(neither occurs) = P(A')P(B') = [1-P(A)}{1-P(B)] = 1/3

Let P(A) = x
Let P(B) = y

Then P(A)*P(B) = 1/6 becomes



and  [1-P(A)}{1-P(B)] = 1/3 becomes



So we have the system of equations:



Solve the 1st equation for y





Simplify the 2nd equation:




Substitute 1/6 for xy



Multiply through by 6






Substitute 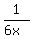 for y





Multiply through by x







2x-1 = 0;  3x-1 = 0
  2x = 1;    3x = 1
   x = 1/2;   x = 1/3

If x = 1/2







and if x = 1/3







So the probabilities are 1/2 and 1/3,
regardless of which is P(A) and which 
is P(B).

So P(A)+P(B) = 1/2+1/3 = 3/6+2/6 = 5/6

Edwin