Question 1042549: One evening, n men enter the restaurant and put their hats at the reception. Each man gets a random hat back
when going back after having dinner. Find the expected number of men who get their right hat back.
A. 1
B. 1/2
C. 1/n
D. n/2
Found 2 solutions by ikleyn, robertb:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One evening, n men enter the restaurant and put their hats at the reception. Each man gets a random hat back
when going back after having dinner. Find the expected number of men who get their right hat back.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It is a good problem and the formulation is good.
But, in order to be solved, it should be reformulated in mathematically correct form.
In my view, this correct formulation is as follows.
Among n! permutations of "n" numbers 1, 2, 3, . . . , n how many are those where the number "k" is in the k-th place (in k-th position) ?
Then the answer is obvious: there are (n-1)! of such permutations.
And we are interested in this ratio 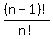 , which is equal to , which is equal to 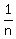 .
Answer. .
Answer. 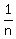 . Option C. . Option C.
On permutations, read the lesson
- Introduction to Permutations
in this site.
Answer by robertb(5830)   (Show Source): (Show Source):
|
|
|