1.Two dice are rolled.
Here are all 36 possible outcomes when two dice are rolled:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
What is the probability that the sum of the outcome is
a.5?
Let's color the ones red that have sum 5:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
I count 4. Therefore the probability is "4 times out of 36" or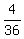 
.
That reduces to 
b.at least 11?
Let's color the ones red that have sum of at least 11:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
I count 3. Therefore the probability is "3 times out of 36" or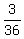 
.
That reduces to 
c.less than 4?
Let's color the ones red that have sum less than 4:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
I count 3. Therefore the probability is "3 times out of 36" or .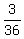
That reduces to
2. Find the point on the graph of f(x)=x^2+4x-3 where the tangent line is horizontal.
The horizontal line through the vertex would be tangent at the
vertex, drawn in green below.
We use the vertex formula:
The x-coordinate of the vertex of f(x) = ax²+bx+c is 
So the x-coordinate of the vertex of f(x) = x²+4x-3 is 
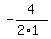= -2.
The y-coordinate is found by substituting the x-coordinate of the
vertex in f(x) = x²+4x-3
f(2) = (-2)²+4∙(-2)-3 = 4-8-3 = -7
So the point on the graph of f(x)=x²+4x-3 where the tangent line is
horizontal is the vertex (-2,-7).
Edwin
