Question 969770: Carbon-14 has a half-life of about 5700 years.
a) Write an equation for the proportion of Carbon-14 remaining in a fossil (relative to the amount of Carbon-14 it had when it was alive) as a function of time "t" in years.
b) Find an equation for the inverse of the function you found in part (a) and say what the inverse does
c) A fossil has 25% of the Carbon-14 it had when it was alive. Give your answer rounded to the nearest year.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Carbon-14 dating is based on the fact that percentage of carbon-14 in the carbon dioxide in the atmosphere is assumed constant, because carbon 14 is created and destroyed at constant stable rates (created by cosmic rays hitting the atmosphere, and destroyed by radioactive decay).
A living creature is constantly incorporating carbon from the environment, and has the same percentage of carbon-14 as its environment.
Once a living creature ceases to live, it ceases to incorporate carbon from the environment, and as the carbon-14 in its body decays at a constant rate, the percentage of carbon present as carbon-14 in that body starts to decrease at the same constant rate.
a)  = years that have passed since the organism died
 = number of carbon-14 half-lives that have passed since the organism died
After one half-life the proportion of Carbon-14 remaining in a fossil (relative to the amount of Carbon-14 it had when it was alive) is
 .
After  half-lives, it is of the previous ,
so it is  of the initial proportion.
After  half-lives, it is of the previous  ,
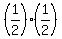so it is  .
After half-lives, it is  .
You can apply all kinds of algebraic manipulations on that expression,
so I do not know where part a) would end.
One such manipulation would be:
 <--> <-->
Maybe that last expression is the expected answer for part a).
b) From ,
or better yet, from  ,
you can find a formula to calculate from  .
<--> <-->
c) Plugging  into the formula  ,
we get  --> 
|
|
|
