Question 936281: Your worst enemy has a new game. He picks a secret polynomial p(x) with positive integer
coefficients the polynomial can have any degree and the coefficients can be arbitrarily big.
You get to name two values of x and he will tell you the exact value of p(x) for both of them.
You don’t have to choose your second value until your enemy tells you p(x) for the first value.
Your challenge is to pick your two values so that from his answers you can name the polynomial.
For instance, his polynomial might be 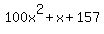 . You might pick x = 3 first, in
which case your enemy would tell you that  . Then you might pick x = .5, and
your enemy would say p(.5) = 182.5. But from this information you can’t determine that
 , because it could also be  , and probably many other
polynomials as well.
Find a strategy by which you can always win this game, and explain (prove) why it works.
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! Here's a solution: Suppose we played the same game, but you are given that your opponent's polynomial's coefficients are in the range {0,1,...,d-1} for some positive integer d. Then you should ask for P(d). Note that the value of P(d) corresponds to a base-d integer, and it is well known that every positive integer has a unique base-d representation with coefficients in {0,1...,d-1}.
For example, if you know that the coefficients of P(x) are in {0,1,...,9}, then d = 10, and suppose P(10) = a*10^3 + b*10^2 + c*10 + d = 2549. Then P(x) = 2x^3 + 5x^2 + 4x + 9.
To find a value of d, first guess P(1), which is the sum of the coefficients. Since the coefficients are positive integers, P(1) >= d, so you should guess P(1) and then P(P(1)).
|
|
|
