Question 819909: List all zeros of the polynomnial function
f(x)= x^5 - 7x^4 + 10x^3 + 26x^2 - 47x - 39
given that x = 3+ 2i
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! The possible rational roots/zeros of  are: are:
+1, +3, +13, +39
Using synthetic division to test these we will find that only one of these, 3, is actually a zero:
3 | 1 -7 10 26 -47 -39
---- 3 -12 -6 60 39
------------------------------
1 -4 -2 20 13 0
Not only does the zero in the lower right indicate that 3 is a zero (and (x-3) is a factor) but the rest of the bottom row tells us the other factor. The "1 -4 -2 20 13" translates into 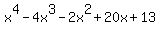 . So . So

As mentioned earlier, none of the other possible rational roots/zeros work. And, if "given that x = 3+ 2i" is supposed to indicate that 3+2i is also a zero, then this is an error. 3+2i is not a zero of f(x)! It is was, then 3-2i would also be a zero. And if they were both zeros then 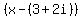 and and 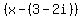 would be factors of f(x). And since would be factors of f(x). And since  , , 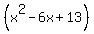 would also be a factor of f(x). And if would also be a factor of f(x). And if 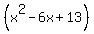 were a factor of f(x) then it would divide evenly into f(x). But it does not!! So either there is an error in what you posted or I am misinterpreting "given that x = 3+ 2i". were a factor of f(x) then it would divide evenly into f(x). But it does not!! So either there is an error in what you posted or I am misinterpreting "given that x = 3+ 2i".
In summary:- x = 3 is the only zero we can find.
- 3+2i (and 3-2i) are not zeros of f(x).
P.S. The only way I know to find approximations for the remaining 4 zeros would be to- Use a graphing calculator to graph f(x) (or
 ) ) - Use the trace function to find approximations for where the graph crosses the x-axis.
|
|
|