Question 610967: What is the end behavior of -x^4+x^2?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, when you are asked to determine the "end behavior" of some expression, you are being asked: "What happens to the value of the expression when the variable becomes very large, positive or negative?" Note: You can get one answer to this question for large positive x's and another for large negative x's.
Second, 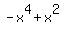 is a polynomial. When determining the end behavior of a polynomial, ignore all terms except the one with the highest exponent. (This is done because for large values, the highest exponent term will "overwhelm" whatever values come from the other terms.) is a polynomial. When determining the end behavior of a polynomial, ignore all terms except the one with the highest exponent. (This is done because for large values, the highest exponent term will "overwhelm" whatever values come from the other terms.)
So we are going to examine what happens to 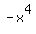 for large positive and large negative numbers. For large positive x's the for large positive and large negative numbers. For large positive x's the  part of part of 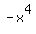 will become an extremely large positive number. And with the "-" in front, will become an extremely large positive number. And with the "-" in front, 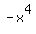 , becomes an extremely large negative number. , becomes an extremely large negative number.
For large negative x's the  part of part of 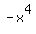 will become an extremely large positive number (remember how even exponents work on negative numbers!). And with the "-" in front, will become an extremely large positive number (remember how even exponents work on negative numbers!). And with the "-" in front, 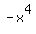 , becomes an extremely large negative number. , becomes an extremely large negative number.
So for both large positive and large negative x's, 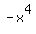 (and therefore (and therefore 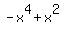 ), will take on extremely large negative values. Graphically this means that the graph of ), will take on extremely large negative values. Graphically this means that the graph of  will go down (to large negative y values) on the right (where x is large and positive) and on the left (where x is large and negative). will go down (to large negative y values) on the right (where x is large and positive) and on the left (where x is large and negative).
|
|
|