Question 136630This question is from textbook Prentice Hall Algebra 2
: Find a fourth-degree polynomial equation with integer coefficients that has the given numbers as roots.
The given numbers are 3+ i and -2i
This question is from textbook Prentice Hall Algebra 2
Found 2 solutions by Fombitz, solver91311:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Complex roots always come in conjugate pairs.
If 3+i is a root, so is 3-i.
If -2i is a root, so is 2i.


Work out the final steps to get the solution.
Post another question if you get stuck.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a polynomial equation has a complex root of the form  , then the conjugate of the complex number, , then the conjugate of the complex number, 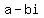 is also a root. Therefore, your four roots are is also a root. Therefore, your four roots are  , ,  , , 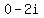 , and , and 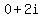
If any number a is a root of a polynomial equation, then  is a factor of the polynomial. Therefore, the factors of your polynomial are is a factor of the polynomial. Therefore, the factors of your polynomial are 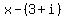 , , 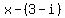 , , 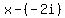 , and , and 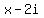 . Just multiply the 4 factors together and you will have your required polynomial. The problem asks for a polynomial equation so remember to set the 4th degree polynomial result equal to 0 at the end. . Just multiply the 4 factors together and you will have your required polynomial. The problem asks for a polynomial equation so remember to set the 4th degree polynomial result equal to 0 at the end.
Hint: Be very careful with your signs when multiplying. Remember that  , so something like , so something like  . .
|
|
|