Question 1192358: a painter wanted to mix 2 liters of blue paint with 3 liters of yellow paint to make 5 liters of green paint. however, by mistake, he used 3 liters of blue and 2 liters of yellow so that he made the wrong shade of green. what is the smallest amount of this green paint that he must throw away so that, using the rest of his green paint, and some extra blue or yellow paint he could make 5 liters of paint of the correct shade of green?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
a painter wanted to mix 2 liters of blue paint with 3 liters of yellow paint to make 5 liters of green paint.
however, by mistake, he used 3 liters of blue and 2 liters of yellow so that he made the wrong shade of green.
what is the smallest amount of this green paint that he must throw away so that,
using the rest of his green paint, and some extra blue or yellow paint he could make 5 liters of paint
of the correct shade of green?
~~~~~~~~~~~~~~
After first (mistaken) mix, the painter has too much blue paint and too little yellow paint in the mixture,
so, OBVIOUSLY, he should add extra yellow paint at some moment.
After first (mistaken) mix, the painter has 5 liters of paint with 2 liters of yellow paint in it,
which contents is 40% = 0.4 of yellow in the total of 5L volume.
He poors out an unknown amount of V liters of the mixed paint and adds V liters of yellow paint.
After it, the painter has 0.4*(5-V)+V liters of yellow paints in the 5 liters total volume.
He wants the ratio 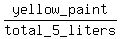 be  = 0.6, i.e.
0.4*(5-V) + V = 0.6*5.
Simplify and find V
2 - 0.4V + V = 3
-0.4V + V = 3 - 2
0.6V = 1
V = 1/0.6 = 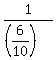 =  =  liters.
ANSWER. = 1.666... liters of the original mistaken mixture should be poored out and replaced with = 1.666... liters of yellow paint.
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is a non-standard method for solving this kind of problem. Compare it to the standard solution shown by the other tutor and see if this method "works" for you.
When we get past all the words in the problem, we see that essentially the problem is mixing some paint that is 2/5 yellow with paint that is all yellow to get paint that is 3/5 yellow.
(1) Look at the three fractions of yellow on a number line -- 2/5, 3/5, and 1 (=5/5).
(2) Observe/calculate that 3/5 is 1/3 of the way from 2/5 to 1.
(3) That means 1/3 of the mixture needs to be the all yellow paint.
(4) The mixture is to be 5 liters, so the amount of all yellow paint in the mixture should be 1/3 of 5 liters, which is 5/3 liters.
ANSWER: 5/3 liters, or 1 2/3 liters, of the original mixture should be thrown away and replaced with yellow paint to get the right shade of green.
|
|
|
