Question 1191999: Form a fifth-degree polynomial function with real coefficients such that 5i, 1-3i, and -3 are zeros and f(0)=1500
Found 3 solutions by Boreal, josgarithmetic, Edwin McCravy:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! complex roots are conjugate
roots are +/-5i
1-3i, 1+3i
-3
Two factors are (x^2+25)(x+3)
The other two are (x+1+3i) (x-1-3i)
multiply those to get x^2-2x+10, which has roots (1/2)(2+/-sqrt(-36)) or (1/2) (2+/-6i)
=x^2-2x+10
a(x^2+25)(x+3)(x^2-2x+10) is the polynomial
when x=0 the value is 25*3*10=750, so a must be 2.
2(x^2+25)(x+3)(x^2-2x+10)
Answer by josgarithmetic(39621)  (Show Source):
You can put this solution on YOUR website! 
Simplify each binomial as necessary, do whatever multiplications you feel you need, and find "a" by substituting 0 for x according to y=1500.
This is a very routine exercise.
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
Instead of doing your problem for you, I'm going to do
one exactly like it instead, step by step. Here's the one I'm
going to do. Use it as a model for yours.
Form a fifth-degree polynomial function with real coefficients
such that 6i, 1-4i, and -4 are zeros and f(0)=7344
If a polynomial with real coefficients has a complex imaginary zero,
its conjugate is also a zero.
Since 6i is a zero, so is -6i.
Since 1-4i is a zero, so is 1+4i.
x-6i, x-(-6i), x-(1-4i), x-(1+4i), x-(-4) are all factors. Simplifying them:
x-6i, x+6i, x-1+4i, x-1-4i, x+4
So f(x) must be some constant "a" times the product of those factors:
  
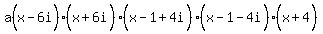Multiply that out:
It makes it a little easier to group the real parts of conjugates:
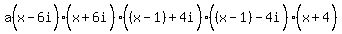
Since i2 = -1
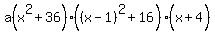
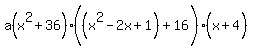
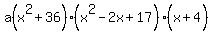
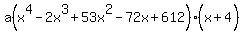
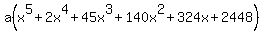Since f(0)=7344,
 
 
 
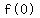
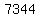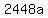
So
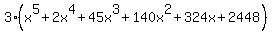
Edwin
|
|
|
