SOLUTION: Let P(x) be a nonconstant polynomial, where all the coefficients are nonnegative integers. Prove that there exist infinitely many positive integers n such that P(n) is composite.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Let P(x) be a nonconstant polynomial, where all the coefficients are nonnegative integers. Prove that there exist infinitely many positive integers n such that P(n) is composite.      Log On


   

Question 1182506: Let P(x) be a nonconstant polynomial, where all the coefficients are
nonnegative integers. Prove that there exist infinitely many positive
integers n such that P(n) is composite.
Hint(s):
Remember that if a and b are distinct integers, then P(a) - P(b) is divisible by a - b.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
when the degree is 1, P(x) = c1x+c2, certainly you can
put in infinitely many positive integers for x and get a composite number.

For P(x) with degrees m > 1:

P%28x%29%22%22=%22%22sum%28c%5Bk%5D%28x%5Ek%29%2Ck=0%2Cm%29, ci ≥ 0.

P%28a%29-P%28b%29%22%22=%22%22sum%28c%5Bk%5D%28a%5Ek%29%2Ck-0%2Cn%29-sum%28c%5Bk%5D%28b%5Ek%29%2Ck=0%2Cm%29%22%22=%22%22sum%28c%5Bk%5D%28a%5Ek-b%5Ek%29%2Ck=0%2Cm%29%22%22=%22%22

sum%28c%5Bk%5D%28a-b%29sum%28a%5E%28k-1-j%29%2Ab%5Ej%2Cj=0%2Ck-1%29+%2Ck=0%2Cm%29%22%22=%22%22%28a-b%29sum%28c%5Bk%5Dsum%28a%5E%28k-1-j%29%2Ab%5Ej%2Cj=0%2Ck-1%29+%2Ck=0%2Cm%29%22%22=%22%22

%28a-b%29%28matrix%281%2C8%2Cthe%2Csum%2Cof%2Ctwo%2C+or%2C+more%2Cpositive%2Cintegers%29%29

There are an infinite number of ways we can choose a and b a > b, such
that a-b is not 1.  And the summation is of two or more positive integers,
which are integers > 1. 

So there exist infinitely many positive integers n such that P(n) is
composite.

Edwin

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

            I saw several proofs to this statement in the  Internet  (including this forum).
            Some of them are defective or unsufficient;  to others,  I don't like them,  since they are not convincing.

            Finally,  I found one in the  Internet,  which is understandable,  correct and convincing at the same time.
            So,  I place it here,  with the reference.  The source is this document
            https://faculty.math.illinois.edu/~hildebr/putnam/training19/polynomials1sol.pdf
            of the  University of  Illinois  Math  Contest  Training  Sessions. 


Let  n0 = P(2)  and note that,  since  P(x)  is non-constant  (i.e., has degree at least 1)  and has nonnegative integer
coefficients,  n0  is an integer ≥ 2. 


Now consider any integer n with n ≡ 2 mod n0. By the general properties of congruences, we have  

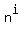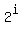    n%5Ei ≡ 2%5Ei mod n0 for any nonnegative integer i, 


and hence 

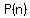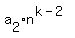    P%28n%29 = a%5B1%5D%2An%5E%28k-1%29 + a%5B2%5D%2An%5E%28k-2%29 + . . .  + a%5Bk%5D%2An%5E0 ≡

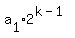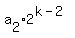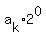         ≡ a%5B1%5D%2A2%5E%28k-1%29 + a%5B2%5D%2A2%5E%28k-2%29 + · · · + a%5Bk%5D%2A2%5E0 = P(2) mod n0. 


Since P(2) = n0,  it follows that  P(n) ≡ 0 mod n0,  so  P(n)  is divisible by  n0  for any such n. 


Moreover, since P has nonnegative coefficients and is non-constant, P(x) is increasing in
x and so P(n) > P(2) = n0 for any n > 2. 


Thus,  n0  is a proper divisor of  P(n)  for any integer  n > 2  with  n ≡ 2 mod n0, 

and  P(n)  is therefore composite for any such n,  i.e.,  for n = 2 + n0,  2 + 2n0, . . . .

The proof is completed.

By the way,  the same proof works for any natural number m > 1  instead of  2,  without any change  ( ! )

-------------

Regarding the  "hint"  at the end of the problem,  I think it is  IRRELEVANT.


////////////


It is  "instructive"  to read about this  UI  Math  Contest  Program from
https://faculty.math.illinois.edu/~hildebr/putnam/ 

    The UI Math Contest Program is one of the most extensive and most visible in the country. 
    It has been considerably expanded in recent years with additional contest opportunities 
    and an enhanced training program, and participation in our events is at record levels. 
    Our students have produced outstanding results in national competitions, culminating 
    in an Honorable Mention for the UI Putnam Team in 2015.


    The William Lowell Putnam Competition is an annual math contest for undergraduates 
    sponsored by the Mathematical Association of America. It has been called the "world's toughest math test", 
    and is widely considered as the most prestigious contest of its kind. More than 4000 students 
    from colleges and universities in the United States and Canada participate in this contest each year.