SOLUTION: Given the expression; x2 - kx + 81 a) Determine the value of "k" that makes it a perfect square trinomial b) Factor it to prove it is factorable.

One solution is OBVIOUS: it is k= 18, found by @MathLover1.

Then  x^2 -18x + 81 = (x-9)*(x-9) = .      (1)



But there is another solution, too:  k= -18, which makes THIS factoring

      x^2 + 18x + 81 = (x+9)*(x+9) = 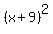.     (2)


And the person, familiar with standard binomial identities 

     (a+b)^2 = a^2 + 2ab + b^2,   (a-b)^2 = a^2 - 2ab + b^2,      (3)

should see it MOMENTARILY (!).



But even more interesting fact is that there are MANY OTHER DECOMPOSITIONS over integer numbers.

They come from decomposition of the number 81 into the product of integer factors

    81 = 1*81 = 3*27 = (-1)*(-81) = (-3)*(-27)          (4)

(I just do not include the cases 81 = 9*9 = (-9)*(-9), which I considered above).



These decompositions produce the following factoring over integer numbers

    81 = 1*81        -->  k = 1 + 81 = 82       -->  x^2 - k + 81 = x^2 - 82 + 81 = (x-1)*(x-81)

    81 = 3*27        -->  k = 3 + 27 = 30       -->  x^2 - k + 81 = x^2 - 30 + 81 = (x-3)*(x-27)

    81 = (-1)*(-81)  -->  k = -1 + (-81) = -82  -->  x^2 - k + 81 = x^2 + 82 + 81 = (x+1)*(x+81)

    81 = (-3)*(-27)  -->  k = -3 + (-27) = -30  -->  x^2 - k + 81 = x^2 + 30 + 81 = (x+3)*(x+27)


So, over integer numbers we have 6 (six, SIX) solutions for k:  18, - 18, 82, -82, 30 and - 30, which provide 

factoring of  x^2 - k + 81 into the product of two binomials.



And if we admit factoring over REAL coefficients, then the number of possible solutions for k becomes INFINITE
(but it is just another melody).


ANSWER.  There are 6 values of k that provide factoring over integer domain.