Question 1124651: Find the quadratic equation function that has the given vertex and goes through the given point. Vertex(1,3), point (-2,0) f(x) =
Found 3 solutions by rothauserc, josmiceli, MathTherapy:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! vertex form of quadratic equation is
:
f(x) = a(x-h)^2 +k, where (h,k) is the vertex
:
we are given the vertex (1,3)
:
f(x) = a(x-1)^2 +3
:
we are given point (-2,0) on the curve
:
a(-2-1)^2 +3 = 0
:
9a +3 = 0
:
9a = -3
:
a = -3/9 = -1/3
:
f(x) = (-1/3)(x-1)^2 +3 =
:
(-1/3)(x^2 -2x +1) +3 =
:
-x^2/3 +2x/3 -1/3 + 3 =
:
-x^2/3 +2x/3 +8/3
:
**************************
f(x) = -x^2/3 +2x/3 +8/3
**************************
:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the quadratic equation function that has the given vertex and goes through the given point. Vertex(1,3), point (-2,0) f(x) =
Since the vertex of and a point on the parabola are given, we use the vertex form of a parabolic equation, or  , with (h, k) being the vertex, and the point (x, y) , with (h, k) being the vertex, and the point (x, y)
 ----- Substituting y for f(x), and then 0 for y, (1, 3) for (h, k), and (- 2, 0) for (x, y) in order to determine "a." ----- Substituting y for f(x), and then 0 for y, (1, 3) for (h, k), and (- 2, 0) for (x, y) in order to determine "a."

0 = 9a + 3
- 3 = 9a_____

 ------- Substituting ------- Substituting 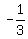 for "a," and (1, 3) for (h, k) for "a," and (1, 3) for (h, k)
|
|
|