|
Question 1039745: Can I please have your assistance? What are the least, and most, amount of distinct zeroes of a 7th degree polynomial, given that at least one root is a complex number?
Found 2 solutions by robertb, Theo:
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! If at least one of the roots is a complex number, then its complex conjugate is also a root of the polynomial. If the complex root has multiplicity 3, then the complex conjugate root would also have multiplicity 3. It would follow that exactly one root would be real, and the 7th degree polynomial would have the form  , ,
where d is the lone real root. In this case the least number of distinct roots is 3.
It is also possible that the polynomial would have three distinct complex roots. If this is the case then the form of the polynomial would be
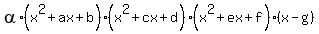 , ,
in which case there would be 7 distinct zeroes, the most number of distinct zeroes. (g is the lone real root.)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the number of roots of the equation has to be equal to the degree of the eqution.
that means, if you have a 7 degree equation, then the number of roots has to be equal to 7 total.
you cannot have just one complex root.
they come in pairs.
you either have two or you have none.
in 7 degree equation, you can have up to 6 complex roots and 1 real root.
if you only have 2 complex roots, then the number of real roots have to be equal to 5, except that you can have a minimum of 1 distinct real root and a maximum of 5 distinct real roots.
by distinct means that the zeroes are different.
(x-5) * (x-5) are two real roots but they have one distinct zero.
(x-5) * (x-6) are two real roots that have two distinct zeroes.
(x-5)^5 are 5 real roots but they have one distinct zero.
if you have two complex roots in a seventh degree equation, you must have 5 real roots, but the distinct real roots can be from 1 to 5.
the following graphs show you what i mean.
all the following graphs are of seventh degree equations.
the graph being displayed is the one with the blue colored circle to the left of it.
the first graph is (x^2 + 2x + 8) * (x-3)^5
there are 2 complex roots and 5 real roots, but only 1 distinct real roots.
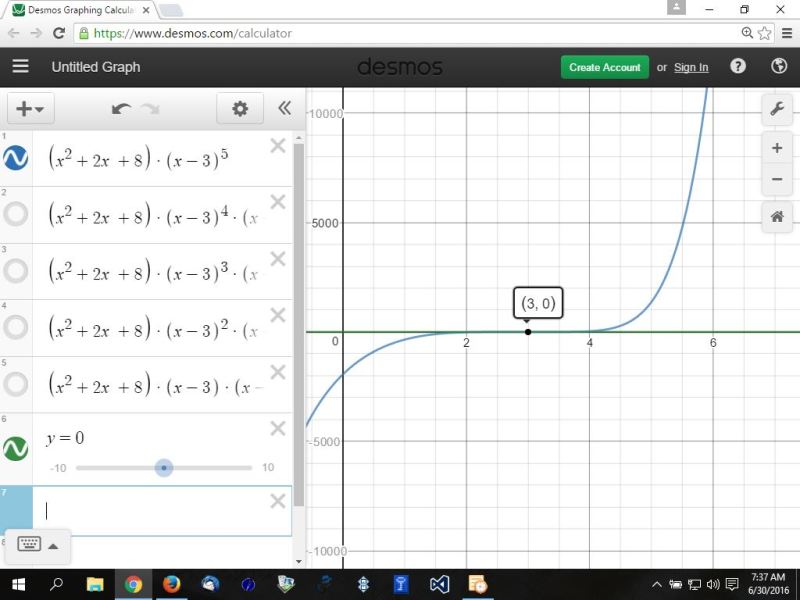
the second graph is (x^2 + 2x + 8) * (x-3)^4 * (x-4)
there are 2 complex roots and 5 real roots, but only 2 distinct real roots.

the third graph is (x^2 + 2x + 8) * (x-3)^3 * (x-4) * (x-5)
there are 2 complex roots and 5 real roots, but only 3 distinct real roots.

the fourth graph is (x^2 + 2x + 8) * (x-3)^2 * (x-4) * (x-5) * (x-6)
there are 2 complex roots and 5 real roots, but only 4 distinct real roots.

the fifth graph is (x^2 + 2x + 8) * (x-3) * (x-4) * (x-5) * x-6) * (x-7)
there are 2 complex roots and 5 real roots, all of which are distinct.

the sixth graph is (x^2 + 2x + 8)^3 * (x-3)
there are 6 complex roots and 1 real root.

the seventh graph is (x^2 + 2x + 8)^2 * (x-3) * (x-4) * (x-5)
there are 4 complex roots and 3 real roots, all of which are distinct.

the eighth graph is the same as the fifth graph.
there are 2 complex roots and 5 real roots, all of which are distinct.

all equations are 7th degree equations.
all equations have 7 roots.
only the real roots cross the x-axis.
the complex roots do not.
for your information, the complex roots of x^2 + 2x + 8 are:
(x - 1 - i*sqrt(7)) and (x - 1 + i*sqrt(7))
these started out as:
(x - 1 - sqrt(-7)) and (x - 1 + sqrt(-7))
sqrt(-7) is the same as sqrt(-1 * 7)
sqrt(-1 * 7) is equal to0 sqrt(-1) * sqrt(7)
sqrt(-1) is equal to i.
sqrt(-7) therefore becomes i * sqrt(7)
replace sqrt(-7) in (x - 1 - sqrt(-7)) and (x - 1 + sqrt(-7)) and you get:
(x - 1 - i*sqrt(7)) and (x - 1 + i*sqrt(7))
if you multiply these factors out, you will get x^2 - 2x + 8
|
|
|
| |