|
Question 1033983: given x is not equal to 7/4 and x is not equal to -1 simplify this rational this rational expression. what is the missing value?
16^2-49/4x^2-3x-7=(4x+7)(4x-7)/(4x-7)(x+1)=______/x+1
Found 2 solutions by stanbon, Theo:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! given x is not equal to 7/4 and x is not equal to -1 simplify this rational this rational expression. what is the missing value?
(16^2-49)/(4x^2-3x-7)
= [(4x+7)(4x-7)]/[(4x-7)(x+1)]
--------------------------
= ((4x+7)/(x+1)
---------------
Cheers,
Stan H.
-------------
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i believe you meant 16x^2 - 49 as the numerator.
your equation becomes:
 . .
the (4x-7) in the numerator and the denominator cancel out and you are left with 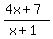 . .
i graphed all 3 equations so you can see what they look like.
the equation i graphed are:
y = 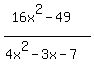
y = 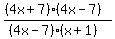
y = 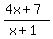
all 3 equation generate the same graph.
there is no difference between the first two equations.
they will generate a vertical asymptote at x = -1 and a hole at x = 7/4.
the third equation is different in that it will not generate a hole at x = 7/4.
this is because, once you cancel out the same factor from the numerator and denominator, the resulting equation doesn't generate a hole because you no longer have a denominator that becomes 0 at that point.
the graph of all 3 equations is shown below.

to determine which equation give you a hole at 7/4, simply replace x with 7/4 in all 3 equations.
the first 2 equations should give you an undefined answer, while the third equation should give you a defined answer for the value of y.
i analyzed all 3 equations by replacing x with 7/4 in my ti-84+ calculator.
the first equation yielded y = divide by 0 error.
the second equation yielded y = divide by 0 error.
the third equation yielded y = 5.09090909....., which is equivalent to 5 + 1/11.
the graph shows you that the graph "appears" to be continuous at x = 7/4, even though there is a hole there for the first 2 equations. it just can't be seen by the naked eye and is only discovered through analysis of the equation at that point.
the ti-84+ calculator will graph it, and has the ability to check for the value of x at certain point by just selecting that value of x.
for the first 2 equations, the ti-84+ will show you that the y value is blank.
this is because there is no value at that point because it is undefined.
for the third equation, the ti-84+ will show you the y-value at that point.
in order to find the hole manually, you need to set the denominator equal to 0 and solve for x.
you also need to factor both numerator and denominator so that the same factor in the numerator and denominator show up.
you can't see that there is a hole by looking at 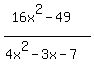 . .
you can see that there is a hole by looking at 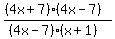
the numerator and denominator have the same factor, indicating there will be hole there and not an asymptote.
there will be an asymptote at x = -1 because the same factor doesn't appear in the numerator.
|
|
|
| |