Question 1023621: Please help and show all work. Thanks
Real Zeros of Polynomials
1. The polynomial of degree 4, P(x) has a root of multiplicity 2 at x=3 and roots of multiplicity 1 at x=0 and x=−2. It goes through the point (5,14).
Find a formula for P(x).
P(x)=
2. The polynomial of degree 3, P(x), has a root of multiplicity 2 at x=5 and root of multiplicity 1 at x=-1. The y-intercept is y=-12.5.
Find a formula for P(x).
P(x)=
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. A polynomial with a root of multiplicity 2 at x=3 has  as a factor. as a factor.
A polynomial with roots of multiplicity 1 at x=0 and x=−2
has  and and  as factors. as factors.
The factors listed make
 , with , with 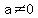 a polynomial f degree 4. a polynomial f degree 4.
If the graph of such polynomial goes through point (5,14), then  ,and ,and  , so , so
 --> --> --> --> --> --> . .
So,  is a formula for such a polynomial. is a formula for such a polynomial.
2. Similarly, the polynomial must be of the form
 , with , with 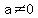 , ,
ana if the y-intercept is 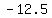 , ,
 must be such that must be such that  . .
So,  --> --> --> --> --> --> --> --> , ,
and  is a formula for such a polynomial. is a formula for such a polynomial.
|
|
|