Question 1074021: The ratio of interior and exterior angles of a polygon is 6:4. Find the sum of the angles of the polygon.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE SHORT WAY:
The ratio given means that it is a polygon
with congruent angles, and at least 5 sides, because
if the angles were not all congruent,
there would be two or more different ratios,
and for 3- and 4-sided polygons with congruent angles,
the ratios are 1:2 and 1:1 respectively.
So, for this polygon, At every vertex,
the ratio of exterior to interior angle,
and the ratio of the sums of exterior and interior angles is 6:4.
The sum of all the exterior angles of any polygon is  , ,
If  = the sum of all interior angles, = the sum of all interior angles,
 ---> --->  ---> --->  . .
ANOTHER WAY (with insights):
The interior and exterior angles at each vertex are supplementary,
meaning that their measures add up to  . .
So, a larger interior angle would be paired with a smaller exterior angle.
If the ratio is 6:4 for the pair of angles at every vertex,
all interior angles in that polygon have the same measure,
and the polygon is equiangular, just like a regular polygon
Except for an equilateral triangles (with just 3 angles)
and rectangles or squares (with just 4 angles),
the exterior angles are smaller than the interior ones
in all regular polygons.
So, if  is the measure of each exterior angle in degrees, is the measure of each exterior angle in degrees,
 is the measier of each interior angle, is the measier of each interior angle,
and  . .
Solving for  : :




The exterior angles are the change in direction
as each vertex as you go around the polygon,
So their measures add up to a whole turn, or  . .
If the polygon has  angles, angles,
then the sum of the measures of the exterior angles (in degrees) is
 --> -->  --> -->  . .
So, the polygon is a pentagon.
The formula for the sum of interior angles for a polygon with
 sides (and sides (and  angles) is angles) is
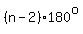 . .
For  , that sum is , that sum is
 . .
|
|
|