Question 1060920: In the given figure, line DB bisects the exterior angle EBA of triangle ABC. If AB = 6, BC = 10, and AC = 12, find DA.
Image is in the link: http://prntscr.com/dhjyfn
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In the given figure, line DB bisects the exterior angle EBA of triangle ABC. If AB = 6, BC = 10, and AC = 12, find DA.
Image is in the link: http://prntscr.com/dhjyfn
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
1. Apply the Cosine Law and find cosine of the angle ABC:
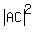 = = 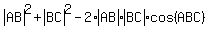 , or , or
 = = 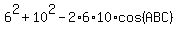 , which gives
cos(ABC) = , which gives
cos(ABC) = 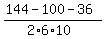 = =  = =  .
In particular, the angle ABC is acute and lies in QI.
2. The angle ABE is the supplement angle to the angle ABC.
Therefore, the angle ABE is obtuse, lies in QII and cos(ABE) = -cos(ABC) = .
In particular, the angle ABC is acute and lies in QI.
2. The angle ABE is the supplement angle to the angle ABC.
Therefore, the angle ABE is obtuse, lies in QII and cos(ABE) = -cos(ABC) = 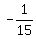 .
3. The angle ABD is the half of the angle ABE.
Find cosine of the angle ABD by applying the formula of cosine of the half angle:
cos(ABD) = .
3. The angle ABD is the half of the angle ABE.
Find cosine of the angle ABD by applying the formula of cosine of the half angle:
cos(ABD) = 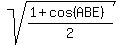 = = 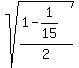 = = 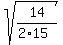 = =  .
4. Let "x" be the length of the segment AD abd "y" be the length of the segment BD: x = |AD|, y = |BD|.
Apply the Cosine Law to the triangle ABD: .
4. Let "x" be the length of the segment AD abd "y" be the length of the segment BD: x = |AD|, y = |BD|.
Apply the Cosine Law to the triangle ABD:
 = = 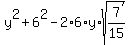 . (1)
Apply the Cosine Law to the triangle CBD: . (1)
Apply the Cosine Law to the triangle CBD:
 = = 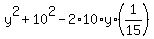 . (2)
5. Now solve the system of two nonlinear equations in two unknowns (1) and (2).
For it, open parentheses in (2) and distract eq.(1) from eq.(2). You will get
24x + 144 = . (2)
5. Now solve the system of two nonlinear equations in two unknowns (1) and (2).
For it, open parentheses in (2) and distract eq.(1) from eq.(2). You will get
24x + 144 =  , or
24x = , or
24x =  . (3)
Now you have one linear equation (3) with the expressed "x" via "y", and the quadratic equation (1).
It is solvable. You can solve it and obtain expressions for "x" and "y".
In this way you will complete the solution and will get the answer. . (3)
Now you have one linear equation (3) with the expressed "x" via "y", and the quadratic equation (1).
It is solvable. You can solve it and obtain expressions for "x" and "y".
In this way you will complete the solution and will get the answer.
|
|
|