SOLUTION: how many sides are there for a regular polygon whose each interior angle is 108 degree

Consider two neighbor vertices of the polygon.
Connect them by segments with the center of the polygon.
You will get an isosceles triangle with one vertex at the center of the polygon.


Then each angle of 108 degs will be bisected in two angles of 54 degs each.
So the angle at the base of your isosceles triangle is 54 degs.

Then the angle of the triangle at the center of the polygon is (180 - 2*54) = 72 degs.

To find the number of sides of the polygon, divide 360 degs by 72: 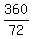 = 5.

Your polygon is a pentagon.