Question 885692: How many different sized triangles can be formed using 2 cm,3cm,4cm,5cm and 6cm rods?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE SOLUTION:
If we have only one rod of each length,  triangles. triangles.
THE EXPLANATION:
Some sets of three rods would determine one triangle.
We can make  such sets, such sets,
but some sets of rods would not make a triangle.
For example, the set of  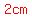    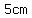  rods, and the set of rods, and the set of  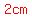    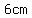 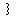 do not make a triangle: do not make a triangle:

To make a triangle, the lengths of the two shorter rods must add up to more than the length of the longest rod.
The set  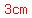    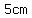  does make a triangle because 3cm + 4cm = 7cm > 5cm : does make a triangle because 3cm + 4cm = 7cm > 5cm :

If we use the 2cm rod, the sets that do not form triangles are
{2cm,3cm,5cm} , {2cm,3cm,6cm} , and {2cm,4cm,6cm} ,
while {2cm,3cm,4cm} , {2cm,4cm,5cm} , and {2cm,6cm,6cm}
All the other sets (without the 2cm rod) form triangles:
{3cm,4cm,5cm} , {3cm,4cm,6cm} , {3cm,5cm,6cm} , and {4cm,5cm,6cm} .
NOTE:
With just one rod of each length we are forced to make scalene triangles (triangles with 3 different side lengths).
If we had 3 (or more) rods of each measure we could make more triangles.
We could make 5 equilateral and 12 isosceles triangles (if I am counting correctly).
|
|
|