1) 1 = 1
2) 2 + 3 + 4 = 1 + 8
3) 5 + 6 + 7 + 8 + 9 = 8 + 27
4) 10 + 11 + 12 + 13 + 14 + 15 + 16 = 27 + 64 = 91
Each left side is an arithmetic series
1. First we make a conjecture about the first term of each
arithmetic series.
Those first terms on the left go 1,2,5,10. Let's compare
that to a list of squares beginning with 0², i.e., 1.2.4.9:
n 1,2,3, 4
an 1,2,5,10
(n-1)² 0,1,4, 9
each number is square of 1 more than the square of 1 less than n
so the general term is (n-1)²+1, or n²-2n+1+1or n²-2n+2.
n²-2n+2
2. Next we make a conjecture about the number of terms in each
arithmetic series.
The number of terms on the left go 1,3,5,7 which is the odd numbers.
We compare them to the even integers, 2n
n 1,2,3,4
an 1,3,5,7
2n 2,4,6,8
We see that each is one less than 2n. So the general term for the
number of terms is 2n-1
3. Next we make a conjecture about the common difference of the
terms of each arithmetic series on the left. That's easy. The
difference is alsways 1.
The formula for the sum of an arithmetic series is
Sn =  [2a1 + (n-1)d]
except in place of n on the right side, we use the general expression
for the number of term. So we replace n by 2n-1. We replace
a1 by the general expression for the first term, n²-2n+2,
and of course d by 1:
Sn =
[2a1 + (n-1)d]
except in place of n on the right side, we use the general expression
for the number of term. So we replace n by 2n-1. We replace
a1 by the general expression for the first term, n²-2n+2,
and of course d by 1:
Sn = 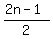 [2(n²-2n+2) + ({2n-1}-1)1], and simplify:
Sn =
[2(n²-2n+2) + ({2n-1}-1)1], and simplify:
Sn = 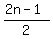 [2n²-4n+4 + (2n-1-1)],
Sn =
[2n²-4n+4 + (2n-1-1)],
Sn = 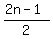 [2n²-4n+4+2n-1-1],
Sn =
[2n²-4n+4+2n-1-1],
Sn = 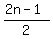 [2n²-2n+2],
Sn =
[2n²-2n+2],
Sn = 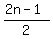 [2(n²-n+1)],
Sn = (2n-1)(n²-n+1)
So (2n-1)(n²-n+1) is the general term for the left side.
Now we look at the right sides. All of them have two terms
except the first, but it can be considered as also having
two terms 0 + 1. So we have
0 + 1, 1 + 8, 8 + 27, 27 + 64. We recognize those as cubes:
0³+1³, 1³+2³, 2³+ 3³, 3³ + 8³
So the general term on the right is (n-1)³+n³
We can factor that as the sum of two cubes:
(n-1)³+n³ = [(n-1)+n]{(n-1)²-(n-1)n+n²] = (n-1+n)(n²-2n+1-n²+n+n²)
= (2n-1)(n²-n+1)
That's the same general term we got for the left side. So we have
proved the conjecture, that in each case the left side will equal
the right side.
Edwin
[2(n²-n+1)],
Sn = (2n-1)(n²-n+1)
So (2n-1)(n²-n+1) is the general term for the left side.
Now we look at the right sides. All of them have two terms
except the first, but it can be considered as also having
two terms 0 + 1. So we have
0 + 1, 1 + 8, 8 + 27, 27 + 64. We recognize those as cubes:
0³+1³, 1³+2³, 2³+ 3³, 3³ + 8³
So the general term on the right is (n-1)³+n³
We can factor that as the sum of two cubes:
(n-1)³+n³ = [(n-1)+n]{(n-1)²-(n-1)n+n²] = (n-1+n)(n²-2n+1-n²+n+n²)
= (2n-1)(n²-n+1)
That's the same general term we got for the left side. So we have
proved the conjecture, that in each case the left side will equal
the right side.
Edwin