Question 368929: 12 boys and 10 girls in which seven students are chosen to go to the blackboard. What is the probability that at least 2 girls are chosen?
C(22,7) = 170,544
I know the answer to this one is 16/17 but how?
I did the long way, need the short way
Long way:
7 b 0g C(12,7) * C(10,0) = 792
6 b 1g C(12,6) * C(10,1) = 9,240
etc...
How do I do the answer in the below format:
C(#,#) C(#,#)
-------------
C(22,7)
A question that relates to the above:
What is the probability that no boys are chosen?
What is the probability that more boys than girls are chosen?
What is the probability that the first three children chosen are boys?
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! 12 boys and 10 girls in which seven students are chosen to go to the blackboard. What is the probability that at least 2 girls are chosen?
1 - (probability of that NOT happening) =
1 - (the probability that all 7 were boys) - (the probability that there was one girl and 6 boys) =
  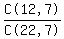  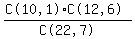        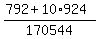    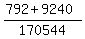  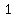  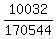  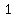    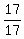    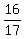
What is the probability that no boys are chosen?
That is the same as all girls are chosen, or 
What is the probability that more boys than girls are chosen?
There isn't any shortcut to this:
P(7boys,0girls) + P(6 boys, 1 girl) + P(5 boys, 2 girls) + P(4 boys, 3 girls)

What is the probability that the first three children chosen are boys?
Choose the first three any 3 of the 12 boys C(12,3) ways, and the other 4 any
of the remaining 19 students, C(19,4), so the probability is
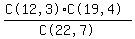 Edwin
Edwin
|
|
|