SOLUTION: suppose there are ten items on a true false test the person taking the test does not read the questions but answers randomly what is the probability of him answering all 10 qestion

This is not a permutation problem.  It deals with the more
general principle of multiplication.

There is only one correct way to get them all right.

So the numerator of the required probability is 1.

Now we calculate the number of ways to answer the test.

There are 2 ways to answer the 1st question.

For each of the 2 ways to answer the 1st question, there 
are 2 ways to answer the 2nd question. So that's 2x2 or 4 
ways to answer the first 2 questions.

For each of the 2x2 or 4 ways to answer the first 2 
questions, there are 2 ways to answer the 3rd question. 
So that's 2x2x2 or 8 ways to answer the first 3 questions. 

For each of the 2x2x2 or 8 ways to answer the first 3 
questions, there are 2 ways to answer the 4th question. 
So that's 2x2x2x2 or 16 ways to answer the first 4 questions.

For each of the 2x2x2x2 or 16 ways to answer the first 4 
questions, there are 2 ways to answer the 5th question. So 
that's 2x2x2x2x2 or 32 ways to answer the first 5 questions.

For each of the 2x2x2x2x2 or 32 ways to answer the first 5 
questions, there are 2 ways to answer the 6th question. So 
that's 2x2x2x2x2x2 or 64 ways to answer the first 6 questions.

For each of the 2x2x2x2x2x2 or 64 ways to answer the first 6 
questions, there are 2 ways to answer the 7th question. So 
that's 2x2x2x2x2x2x2 or 128 ways to answer the first 7 
questions.

For each of the 2x2x2x2x2x2x2 or 128 ways to answer the first 
7 questions, there are 2 ways to answer the 8th question. 
So that's 2x2x2x2x2x2x2x2 or 256 ways to answer the first 8 
questions.

For each of the 2x2x2x2x2x2x2x2 or 256 ways to answer the first 
8 questions, there are 2 ways to answer the 9th question. So 
that's 2x2x2x2x2x2x2x2x2 or 512 ways to answer the first 9 
questions. 

For each of the 2x2x2x2x2x2x2x2 or 512 ways to answer the first 
9 questions, there are 2 ways to answer the 10th question. So 
that's 2x2x2x2x2x2x2x2x2x2 or 1024 ways to answer all 10 
questions. 

So the denominator of the required probability is 
2x2x2x2x2x2x2x2x2x2 or 210 or 1024

The desired probability is 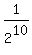 or .

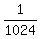Edwin