Question 1204565: A gym class has 12 students, 6 girls and 6 boys. The teacher has 4 jerseys in each of 3 colors to mark 3 teams for a soccer tournament. If the teacher wants at least one girl and at least one boy on each team, how many ways can he give out the jerseys? (Jerseys of the same color are indistinguishable.)
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A gym class has 12 students, 6 girls and 6 boys. The teacher has 4 jerseys in each of 3 colors
to mark 3 teams for a soccer tournament.
If the teacher wants at least one girl and at least one boy on each team, how many ways
can he give out the jerseys? (Jerseys of the same color are indistinguishable.)
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The question in the problem is totally equivalent to this one, which sounds more naturally.
If the teacher wants at least one girl and at least one boy on each team,
in how many ways can he form 3 teams of 4 students in each?
Why it is equivalent? Because team affiliation replaces (= determines) color.
Since the teacher wants at least one girl and at least one boy on each team,
from this restriction it is easy understand that there are two basic configurations of teams
1st configuration : all/(each) three teams are (2 girls, 2 boys);
2nd configuration : the three teams are of these types
one team is (1 girl, 3 boys); other team is (2 girls, 2 boys); third team is (3 girls, 1 boy).
There are no other configurations.
Now let's calculate the number of different ways to form the teams.
1st configuration:
Team 1: 2 girls from 6; 2 boys from 6:
the number of different possible combinations is 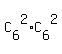 = 15*15 = 225.
Team 2: 2 girls from remaining 4 girls; 2 boys from remaining 4 boys:
the number of different possible combinations is = 15*15 = 225.
Team 2: 2 girls from remaining 4 girls; 2 boys from remaining 4 boys:
the number of different possible combinations is 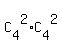 = 6*6 = 36.
Team 3: only one possible combination from remaining 2 girls and 2 boys.
Resume: there are 225 * 36 * 1 = 8100 possible teams of this kind.
2nd configuration:
Team 1: 1 girls from 6; 3 boys from 6:
the number of different possible combinations is = 6*6 = 36.
Team 3: only one possible combination from remaining 2 girls and 2 boys.
Resume: there are 225 * 36 * 1 = 8100 possible teams of this kind.
2nd configuration:
Team 1: 1 girls from 6; 3 boys from 6:
the number of different possible combinations is 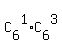 = 6*20 = 120.
Team 2: 2 girls from remaining 5 girls; 2 boys from remaining 3 boys:
the number of different possible combinations is = 6*20 = 120.
Team 2: 2 girls from remaining 5 girls; 2 boys from remaining 3 boys:
the number of different possible combinations is 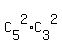 = 10*3 = 30.
Team 3: only one possible combination from remaining 3 girls and 1 boy.
Resume: there are 120 * 30 * 1 = 3600 possible teams of this kind.
Finally, the answer to the problem is this sum 8100 + 3600 = 11700.
+-------------------------------------------------------------------+
| Each way to form 3 teams does correspond to one way |
| to distribute the jerseys. This correspondence is one-to-one |
| in both directions. |
+-------------------------------------------------------------------+
ANSWER. There are 11700 different ways for the teacher to give out the jerseys. = 10*3 = 30.
Team 3: only one possible combination from remaining 3 girls and 1 boy.
Resume: there are 120 * 30 * 1 = 3600 possible teams of this kind.
Finally, the answer to the problem is this sum 8100 + 3600 = 11700.
+-------------------------------------------------------------------+
| Each way to form 3 teams does correspond to one way |
| to distribute the jerseys. This correspondence is one-to-one |
| in both directions. |
+-------------------------------------------------------------------+
ANSWER. There are 11700 different ways for the teacher to give out the jerseys.
Solved.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
|
|
|