Question 1204437: A car license plate contains three letters followed by four digits. How many different plates can be made if no two consecutive letters can be the same, if the letters I, O and Q cannot be used, and if the number 0 cannot be used?
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A car license plate contains three letters followed by four digits.
How many different plates can be made if no two consecutive letters can be the same,
if the letters I, O and Q cannot be used, and if the number 0 cannot be used?
~~~~~~~~~~~~~~~~~~~~
In all, 26-3 = 23 letters and 10-1 = 9 digits are used.
Under imposed conditions, the letters give us the factors 23*22*22;
the digits give the factors 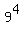 .
So, the final number of all possible plates is .
So, the final number of all possible plates is 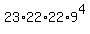 = 73,037,052. ANSWER = 73,037,052. ANSWER
Solved.
|
|
|