Question 1157684: Three dice are tossed. Find the probability of rolling a sum greater than 5.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! Three dice are tossed. Find the probability of rolling a sum greater than 5.
We find the probability of the complement and subtract from 1.
 There are only 10 possible rolls with sums that are NOT greater than 5.
They are these:
1. (1,1,1)
2. (1,1,2)
3. (1,1,3)
4. (1,2,1)
5. (1,2,2)
6. (1,3,1)
7. (2,1,1)
8. (2,1,2)
9. (2,2,1)
10. (3,1,1)
So the numerator (before reducing) of the probability of the complement event
is 10.
We calculate the number of ways the dice can land.
The first one can land any of 6 ways.
For every way the first one can land, the second one can land 6 ways.
So the first two can land 6∙6 or 36 ways.
For every way the first two can land, the third one can land 6 ways.
So there are 6∙6∙6 = 36∙6 = 216 ways the three dice can land.
So the denominator (before reducing) of the probability of the complement event
is 216.
There are only 10 possible rolls with sums that are NOT greater than 5.
They are these:
1. (1,1,1)
2. (1,1,2)
3. (1,1,3)
4. (1,2,1)
5. (1,2,2)
6. (1,3,1)
7. (2,1,1)
8. (2,1,2)
9. (2,2,1)
10. (3,1,1)
So the numerator (before reducing) of the probability of the complement event
is 10.
We calculate the number of ways the dice can land.
The first one can land any of 6 ways.
For every way the first one can land, the second one can land 6 ways.
So the first two can land 6∙6 or 36 ways.
For every way the first two can land, the third one can land 6 ways.
So there are 6∙6∙6 = 36∙6 = 216 ways the three dice can land.
So the denominator (before reducing) of the probability of the complement event
is 216.
 Edwin
Edwin
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The entire space of events has 6*6*6 = 216 elements/(events) with the probability  each.
Of them undesired are
1 event with the sum of 3 [ the event (1,1,1) ]
3 events with the sum of 4 [ the events (1,1,2), (1,2,1) and (2,1,1) ]
6 events with the sum of 5 [ the events (1,1,3), (1,3,1), (3,1,1),
(1,2,2), (2,1,2), (2,2,1) ].
The rest 216 - 10 = 206 events are favorable.
Therefore, the probability under the question is P = each.
Of them undesired are
1 event with the sum of 3 [ the event (1,1,1) ]
3 events with the sum of 4 [ the events (1,1,2), (1,2,1) and (2,1,1) ]
6 events with the sum of 5 [ the events (1,1,3), (1,3,1), (3,1,1),
(1,2,2), (2,1,2), (2,2,1) ].
The rest 216 - 10 = 206 events are favorable.
Therefore, the probability under the question is P = 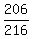 = = 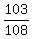 = 0.9537 = 95.37%. ANSWER = 0.9537 = 95.37%. ANSWER
Solved.
|
|
|