|
Tutors Answer Your Questions about Percentage-and-ratio-word-problems (FREE)
Question 1210397: Andrew bought some apples and pears. The ratio of the number of apples bought to the number of pears bought was 7:4. He spent $61.20. He paid $22.80 more for the apples than the pears. Each apple was $0.30 more than each pears.
(a) How much did he spend on the pears?
(b) How many pears did he buy?
Found 4 solutions by MathTherapy, greenestamps, ikleyn, josgarithmetic:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Andrew bought some apples and pears. The ratio of the number of apples bought to the number of pears bought was 7:4. He spent $61.20. He paid $22.80 more for the apples than the pears. Each apple was $0.30 more than each pears.
(a) How much did he spend on the pears?
(b) How many pears did he buy?
Let multiplicative factor be x
As ratio of apples to pears is 7:4, number of apples and pears purchased = 7x and 4x, respectively
Let amount spent on pears be p
Since $22.80 more was spent on apples than pears, then amount spent on apples = p + $22.80
A total of $61.20 was spent, so we then have: p + p + 22.8 = 61.2
2p = 61.2 - 22.8
2p = 38.4
p, or amount spent on pears =  Since $19.20 was spent on “4x” pears, then cost of each pear =
Since $19.20 was spent on “4x” pears, then cost of each pear =  As $19.20 was spent on pears, $61.20 - $19.20, or $42 was spent on “7x” apples, and so, each apple cost
As $19.20 was spent on pears, $61.20 - $19.20, or $42 was spent on “7x” apples, and so, each apple cost  Now, since each apple was $0.30 more than each pear, we get:
Now, since each apple was $0.30 more than each pear, we get:  6 = .3x + 4.8 ---- Multiplying by LCD, x
6 - 4.8 = .3x
1.2 = .3x
x, or multiplicative factor =
6 = .3x + 4.8 ---- Multiplying by LCD, x
6 - 4.8 = .3x
1.2 = .3x
x, or multiplicative factor =  Number of pears purchased: 4x = 4(4) = 16
Number of pears purchased: 4x = 4(4) = 16
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! This is not very neat and much likely not the best way, but this should work.
PRICE QUANTY COST
Apple p+0.3 7x 7x(p+0.3)
Pear p 4x 4x*p
Totals 61.20
and too, the 22.8 dollars difference

Question 1210396: Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins. Then he spent 4/5 of the remaining money on 15 pieces of waffle. Each cupcake cost 2/3 as much as a muffin. Each piece of waffle cost $0.20 more than a cupcake. What was the cost of a muffin?
Found 3 solutions by MathTherapy, mccravyedwin, greenestamps:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins. Then he spent 4/5 of the remaining money on 15 pieces of waffle. Each cupcake cost 2/3 as much as a muffin. Each piece of waffle cost $0.20 more than a cupcake. What was the cost of a muffin?
Let amount spent, be D, cost of a muffin, M, and cost of a cupcake. C
For the first purchase, we get:  3D = 24C + 64M ---- Multiplying by LCD, 8 ---- eq (i)
For the second purchase, we get:
3D = 24C + 64M ---- Multiplying by LCD, 8 ---- eq (i)
For the second purchase, we get:


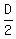 = 15W ---- eq (ii)
Each cupcake cost = 15W ---- eq (ii)
Each cupcake cost  as much as a muffin, so: C = as much as a muffin, so: C =  ---- eq (iii)
Each piece of waffle cost $0.20 more than a cupcake, so: W = ---- eq (iii)
Each piece of waffle cost $0.20 more than a cupcake, so: W = 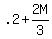 ---- eq (iv) ---- eq (iv)
 ------ eq (ii) ------ eq (ii)
 ---- Substituting ---- Substituting 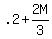 for W, in eq (ii) for W, in eq (ii)
 D = 6 + 20M ---- Multiplying by LCD, 2 ---- eq (v)
3D = 24C + 64M ------ eq (i)
D = 6 + 20M ---- Multiplying by LCD, 2 ---- eq (v)
3D = 24C + 64M ------ eq (i)
 --- Substituting --- Substituting 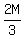 for C, in eq (i)
3D = 8(2M) + 64M
3D = 16M + 64M
3D = 80M ---- eq (vi)
D = 6 + 20M ---- eq (v)
3D = 80M ---- eq (vi)
3D = 18 + 60M ---- Multiplying eq (v) by 3 ---- eq (vii)
0 = - 18 + 20M --- Subtracting eq (vii) from eq (vi)
- 20M = - 18
Cost of a muffin, or for C, in eq (i)
3D = 8(2M) + 64M
3D = 16M + 64M
3D = 80M ---- eq (vi)
D = 6 + 20M ---- eq (v)
3D = 80M ---- eq (vi)
3D = 18 + 60M ---- Multiplying eq (v) by 3 ---- eq (vii)
0 = - 18 + 20M --- Subtracting eq (vii) from eq (vi)
- 20M = - 18
Cost of a muffin, or 
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Most tutors, including me, often ignore where it says this:
"Also, if possible, provide a 'check' at the end, so check if the values
you computed in fact are correct".
Nearly always, we skip this check.
If we would read and heed that, then perhaps we might use a different
method, to make it easier to check.
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins. Then he spent 4/5
of the remaining money on 15 pieces of waffle. Each cupcake cost 2/3 as much as
a muffin. Each piece of waffle cost $0.20 more than a cupcake. What was the
cost of a muffin?
Let T = total money Hakim had at the beginning.
Let C = cost of a cupcake
Let M = cost of a muffin
Let W = cost of a piece of waffle
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins.
 Then he spent 4/5 of the remaining money
which was
Then he spent 4/5 of the remaining money
which was 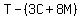 on 15 pieces of waffle.
on 15 pieces of waffle.
 Each cupcake cost 2/3 as much as a muffin.
Each cupcake cost 2/3 as much as a muffin.
 Each piece of waffle cost $0.20 more than a cupcake.
Each piece of waffle cost $0.20 more than a cupcake.

 Go to any of the online solvers for systems of equations
https://www.wolframalpha.com/
https://www.symbolab.com/solver/system-of-equations-calculator
https://cowpi.com/math/systemsolver/4x4.html
https://www.wolframalpha.com/calculators/system-equation-calculator
There are others also.
Type in
(3/8)T = 3C + 8M, (4/5)(T-(3C+8M))=15W, C = (2/3)M, W = C+0.20
Press ENTER, get
C = 0.6, M = 0.09, T = 24, W = 0.8
which we interpret as
C = $0.60, M = $0.90, T = $24.00, W = $0.80.
What was the cost of a muffin?
$0.90 <--- solved, but not checked.
Now let's check:
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins.
(3/8)x$24.00 = $9.00
3x$0.60 = $1.80, 8x$0.90 = $7.20, $1.80 + $7.20 = $9.00.
That checks.
So his remaining money was $24.00 - $9.00 = $15.00
Then he spent 4/5 of the remaining money
which was (4/5)x$15.00 = $12.00
on 15 pieces of waffle.
15x$0.80 = $12.00 and, indeed, that checks.
Each cupcake cost 2/3 as much as a muffin.
$0.60 = (2/3)($0.90)
$0.60 = $0.60, so that checks.
Each piece of waffle cost $0.20 more than a cupcake.
$0.80 = $0.60 + $0.20
$0.80 = $0.80, so that checks.
Now, as you see, everything checks.
Edwin
Go to any of the online solvers for systems of equations
https://www.wolframalpha.com/
https://www.symbolab.com/solver/system-of-equations-calculator
https://cowpi.com/math/systemsolver/4x4.html
https://www.wolframalpha.com/calculators/system-equation-calculator
There are others also.
Type in
(3/8)T = 3C + 8M, (4/5)(T-(3C+8M))=15W, C = (2/3)M, W = C+0.20
Press ENTER, get
C = 0.6, M = 0.09, T = 24, W = 0.8
which we interpret as
C = $0.60, M = $0.90, T = $24.00, W = $0.80.
What was the cost of a muffin?
$0.90 <--- solved, but not checked.
Now let's check:
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins.
(3/8)x$24.00 = $9.00
3x$0.60 = $1.80, 8x$0.90 = $7.20, $1.80 + $7.20 = $9.00.
That checks.
So his remaining money was $24.00 - $9.00 = $15.00
Then he spent 4/5 of the remaining money
which was (4/5)x$15.00 = $12.00
on 15 pieces of waffle.
15x$0.80 = $12.00 and, indeed, that checks.
Each cupcake cost 2/3 as much as a muffin.
$0.60 = (2/3)($0.90)
$0.60 = $0.60, so that checks.
Each piece of waffle cost $0.20 more than a cupcake.
$0.80 = $0.60 + $0.20
$0.80 = $0.80, so that checks.
Now, as you see, everything checks.
Edwin
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1170245: 1.a) Deduce that the total surface area S of a cylinder closed at both ends with height, H and base radius R is given by: S=2πR(R+H) where π is a constant.
b) Find the volume of S given that H =15.0m and R =5.0m (leaving your answer in terms of π)
c) Calculate the amount of water the tank can hold leaving your answer in terms of π.
d) Calculate the height (h) of a cuboid tank of cross-sectional area 25 metre cube which has the same capacity as the cylinder tank in (c) above.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In your post, in the last question, you write
". . . cross-sectional area 25 metre cube . . . ".
Dear missis or mister writer, the area is NEVER measures in "metre cube ".
The appropriate unit for the area is " square meter ".
As I noticed from your posts, you make this error systematically.
It tells me a lot about mathematical qualification of a person who created this problem.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step.
**1.a) Deduce the Total Surface Area of a Closed Cylinder**
* **Area of the Top and Bottom Circles:** Each circle has an area of πR². Since there are two circles (top and bottom), their combined area is 2πR².
* **Lateral Surface Area (Curved Surface):** Imagine unrolling the side of the cylinder. This forms a rectangle with height H and width equal to the circumference of the base (2πR). Therefore, the lateral surface area is 2πRH.
* **Total Surface Area (S):** To find the total surface area, add the areas of the top, bottom, and lateral surfaces:
S = 2πR² + 2πRH
S = 2πR(R + H)
**1.b) Find the Volume of the Cylinder**
* **Volume Formula:** The volume (V) of a cylinder is given by V = πR²H.
* **Given Values:** H = 15.0 m and R = 5.0 m.
* **Calculation:**
V = π(5.0 m)²(15.0 m)
V = π(25 m²)(15.0 m)
V = 375π m³
**1.c) Calculate the Amount of Water the Tank Can Hold**
The amount of water the tank can hold is equal to its volume.
* **Answer:** The tank can hold 375π m³ of water.
**1.d) Calculate the Height of a Cuboid Tank with the Same Capacity**
* **Cuboid Volume Formula:** The volume of a cuboid is given by V = Area of base × height.
* **Given Information:**
* Volume of the cuboid = Volume of the cylinder = 375π m³
* Cross-sectional area (base area) of the cuboid = 25 m²
* **Calculation:**
375π m³ = 25 m² × h
h = (375π m³) / (25 m²)
h = 15π m
**Answers:**
a) S = 2πR(R + H)
b) V = 375π m³
c) 375π m³
d) h = 15π m
Question 1168192: Kameron paid $3.60 for a book. It was marked down 50% of its original price, and he also used a coupon to save an additional 40% off of the sale price. What was the original price?
Write the answer rounded to the nearest cent. Do not include a $ sign.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1168190: Bummer! Kai lives in California and of course, he has to pay sales tax! The sales tax rate is 8.75%. Now, does he have enough money to bring the backpack of his dream home?
(Original price: $88.95, 40% off and Kai has $55.00 saved up so far.)
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1169039: Picture frame has its length 8cm longer than its width. It has an inner 1-cm boundary such that a maximum 660cm^2- picture may fit into it. Find the dimension of this frame.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Picture frame has its length 8cm longer than its width. It has an inner 1-cm boundary
such that a maximum 660cm^2- picture may fit into it. Find the dimension of this frame.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The problem formulation as it is given in the post is INCORRECT.
The correct formulation, in my version, is THIS
Picture frame has its length 8cm longer than its width. It has an inner 1-cm boundary
such that the area of the picture itself is 660cm^2. Find the dimension of this frame.
Below is my solution for this edited formulation.
Since the width of the frame is uniform and since the outer length of the frame is 8 cm longer
than its outer width, the length of the picture itself, without considering the frame, is
8 cm longer than the picture width.
So, if x is the picture width, in centimeters, then the picture length is (x+8) cm,
and we have this equation
x*(x+8) = 660 cm^2. (1)
Now you can guess mentally the solution to this equation: it is x= 22 cm for the picture width,
giving 22+8 = 30 cm for the picture length.
After this guessing, note that the left side of the equation (1) is the monotonic function,
so the guessed solution is UNIQUE.
Alternatively, you can solve this quadratic equation (1) formally, using factoring or the quadratic formula.
In either case, you will get the same solution for x.
Thus the picture is 22 x 30 centimeters.
It implies that the outer dimensions of the frame are 24 x 32 cm.
ANSWER. The outer dimensions of the frame are 24 x 32 cm.
Solved.
Question 1170408: Good day may you please help me with the following question.
Twenty percent of a mixture of pure milk and water is water. Half liter of wine is added to one liter of the mixture of water and milk and thoroughly mixed. What percentage of the new mixture is water?
Found 2 solutions by greenestamps, josgarithmetic:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Total amount of mixture: one liter plus half a liter = 1.5 liters
Amount of water: 20% of one liter = 0.2 liters
Fraction of mixture that is water: 0.2/1.5 = 2/15
Percentage of mixture that is water: 100(2/15) = 200/15 = 40/3 = 13 1/3
ANSWER: 13 1/3%
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1170948: A man would like to invest P 50,000 in government bonds and stocks that will give an
overall annual return of about 5%. The money to be invested in government bonds will
give an annual return of 4.5% and the stocks of about 6%. The investments are in units
of P 100.00 each. If he desires to keep his stock investment to minimum in order to
reduce his risk, determine how many government bonds and how many stocks should he
purchase.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step.
**1. Define Variables:**
* Let 'x' be the number of units of government bonds.
* Let 'y' be the number of units of stocks.
**2. Set Up Equations:**
* **Total Investment:** The total investment is P 50,000, and each unit is P 100.00.
* 100x + 100y = 50,000
* Divide by 100: x + y = 500 (Equation 1)
* **Annual Return:** The desired overall return is 5% of P 50,000, which is P 2,500.
* 4.5% of (100x) + 6% of (100y) = 2,500
* 4.5x + 6y = 2,500 (Equation 2)
**3. Solve the System of Equations:**
We can solve this system using substitution or elimination. Let's use substitution:
* From Equation 1: y = 500 - x
* Substitute this into Equation 2:
* 4.5x + 6(500 - x) = 2,500
* 4.5x + 3,000 - 6x = 2,500
* -1.5x = -500
* x = 500 / 1.5 = 1000 / 3 ≈ 333.33
Since the investments are in whole units, we need to round to the nearest whole number. We'll round down to minimize stock investment, so x = 333.
* Substitute x = 333 back into Equation 1:
* 333 + y = 500
* y = 500 - 333 = 167
**4. Check the Solution:**
* Total Investment: 333(100) + 167(100) = 33,300 + 16,700 = 50,000 (Correct)
* Annual Return:
* (0.045 * 33,300) + (0.06 * 16,700) = 1,498.50 + 1,002 = 2,500.50
The return is slightly over P 2,500, which is acceptable.
**5. Conclusion:**
The man should purchase:
* **333 units of government bonds (P 33,300)**
* **167 units of stocks (P 16,700)**
Question 1177674: A model of the base of PBCom Tower in Ayala is a square whose sides measure 28 m. The intent was to make a side that measures 2,805 m. What is the ratio of the square base of the model to the length of the base side of the intended building?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem:
**1. Understand the Dimensions**
* **Model Side:** 28 meters
* **Intended Building Side:** 2,805 meters
**2. Calculate the Ratio**
The ratio we need is the model side length to the intended building side length:
* Ratio = (Model Side) / (Intended Building Side)
* Ratio = 28 m / 2,805 m
**3. Simplify the Ratio**
Now, let's simplify the fraction:
* 28 / 2,805 ≈ 0.009982174688057042
**4. Express the Ratio**
We can also express this ratio as a fraction.
* 28/2805. We can simplify this fraction by dividing both numerator and denominator by their greatest common divisor, which is 1. Therefore the simplest form of the ratio is 28/2805.
**Answer**
The ratio of the square base of the model to the length of the base side of the intended building is approximately 0.009982 or 28/2805.
Question 1177676: Students in University of the Philippines built a replica of the NCR on a 45.5-ft diameter globe using a scale of 1: 2,000,000. About how tall is the Mount Everest on the model?
(Note: Mount Everest stands 29,000 feet approximately).
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step.
**1. Understand the Scale**
The scale is 1:2,000,000. This means that 1 unit on the model represents 2,000,000 units in reality.
**2. Convert Mount Everest's Height to the Model's Scale**
* Mount Everest's height: 29,000 feet
* Scale: 1:2,000,000
To find the height on the model, we need to divide the actual height by the scale factor:
* Model height (in feet) = 29,000 feet / 2,000,000
* Model height = 0.0145 feet
**3. Convert Model Height to Inches**
Since it's more practical to express small heights in inches, we'll convert feet to inches:
* 1 foot = 12 inches
* Model height (in inches) = 0.0145 feet * 12 inches/foot
* Model height ≈ 0.174 inches
**4. Interpret the Result**
The height of Mount Everest on the model is approximately 0.174 inches.
**Therefore, Mount Everest is about 0.174 inches tall on the model.**
Question 1179673: There are various formulas for calculating ideal body weight. In each of the formulas in this exercise, W is ideal body weight in kilograms, and x is height in inches above 60 in.
Suppose one researcher gave the following formula for men:
W = 51 + 1.9x.
Suppose another researcher published a slightly different formula for men:
W = 55.2 + 1.44x.
At what height do both formulas give the same ideal body weight? Round to the nearest whole number.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step:
**1. Set the Formulas Equal:**
We want to find the height (x) where both formulas give the same ideal body weight (W). So we set the two formulas equal to each other:
51 + 1.9x = 55.2 + 1.44x
**2. Solve for x:**
* Subtract 1.44x from both sides:
51 + 0.46x = 55.2
* Subtract 51 from both sides:
0.46x = 4.2
* Divide by 0.46:
x = 4.2 / 0.46
x ≈ 9.13
**3. Round to the Nearest Whole Number:**
* x ≈ 9 inches
**4. Calculate the Height in Total Inches:**
* Remember that x is the height in inches above 60 inches.
* Total height = 60 + x
* Total height = 60 + 9 = 69 inches
**Answer:**
Both formulas give the same ideal body weight at a height of 69 inches.
Question 1179675: For using a computerized financial news network for 45 min during prime time and 80 min during non-prime time, a customer was charged $11.85. A second customer was charged $15.20 for using the network for 65 min of prime time and 90 min of non-prime time. Find the cost per minute for using the financial news network during prime time.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
**1. Set up the Equations:**
* Let 'x' be the cost per minute for prime time.
* Let 'y' be the cost per minute for non-prime time.
We can create two equations based on the given information:
* Equation 1: 45x + 80y = 11.85
* Equation 2: 65x + 90y = 15.20
**2. Solve the System of Equations:**
We can use various methods to solve this, such as substitution or elimination. Here, I'll use elimination:
* Multiply Equation 1 by 9: 405x + 720y = 106.65
* Multiply Equation 2 by 8: 520x + 720y = 121.60
* Subtract the first modified equation from the second:
* (520x - 405x) + (720y - 720y) = 121.60 - 106.65
* 115x = 14.95
* Solve for x:
* x = 14.95 / 115
* x = 0.13
**3. Find the Value of y (optional):**
* Substitute x = 0.13 into Equation 1:
* 45(0.13) + 80y = 11.85
* 5.85 + 80y = 11.85
* 80y = 6
* y = 6 / 80
* y = 0.075
**Answer:**
The cost per minute for using the financial news network during prime time is $0.13.
Question 1179762: A roller coaster has 3 trains with 8 rows per train. Riders stand in rows of 4, for a total of 32 rider per train. The operators of the coaster recorded the number of riders on each train during a run. On the first train, the operators reported that 7 1/4 rows were filled. On the second train, all 8 rows were filled, and on the third train, 5 1/2 rows were filled.
1. How many more rows were filled on the first train than on the third train?
2. How many rows were empty on the first train? How many additional rider would it take to fill the empty rows? Explain your answer.
3. How many rows were empty on the third train? How many additional riders would it take to fill the empty rows? Explain your answer.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this roller coaster problem step-by-step:
**1. How many more rows were filled on the first train than on the third train?**
* First train: 7 1/4 rows = 7.25 rows
* Third train: 5 1/2 rows = 5.5 rows
* Difference: 7.25 - 5.5 = 1.75 rows
**Answer:** 1.75 more rows were filled on the first train than the third train.
**2. How many rows were empty on the first train? How many additional riders would it take to fill the empty rows? Explain your answer.**
* Total rows per train: 8
* Rows filled on the first train: 7 1/4 rows = 7.25 rows
* Empty rows: 8 - 7.25 = 0.75 rows
* Riders per row: 4
* Additional riders needed: 0.75 rows * 4 riders/row = 3 riders
**Answer:** 0.75 rows were empty on the first train. It would take 3 additional riders to fill the empty rows.
**Explanation:** Since there are 4 riders per row, and 0.75 of a row is empty, we multiply 0.75 by 4 to find the number of riders needed to fill the empty space.
**3. How many rows were empty on the third train? How many additional riders would it take to fill the empty rows? Explain your answer.**
* Total rows per train: 8
* Rows filled on the third train: 5 1/2 rows = 5.5 rows
* Empty rows: 8 - 5.5 = 2.5 rows
* Riders per row: 4
* Additional riders needed: 2.5 rows * 4 riders/row = 10 riders
**Answer:** 2.5 rows were empty on the third train. It would take 10 additional riders to fill the empty rows.
**Explanation:** Since there are 4 riders per row, and 2.5 rows are empty, we multiply 2.5 by 4 to find the number of riders needed to fill the empty space.
Question 1184115: Andy, Berlin and Cheryl had a total of 6750 stamps. At first, Andy have 50%
of his stamps to Berlin. Berlin then gave 1/3 of her stamps to Cheryl.
Finally, Cheryl gave 1/6 of her stamps to Andy. In the end, the ratio of the
number of Andy’s stamps to the number of Berlin’s stamps became 4:5.
Cheryl had twice the total number of stamps that Andy and Berlin had.
How many stamps did Berlin and Cheryl have in total at first?
Found 3 solutions by ikleyn, MathTherapy, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Andy, Berlin and Cheryl had a total of 6750 stamps.
(1) At first, Andy have 50% of his stamps to Berlin.
(2) Berlin then gave 1/3 of her stamps to Cheryl.
(3) Finally, Cheryl gave 1/6 of her stamps to Andy.
In the end, the ratio of the number of Andy’s stamps to the number
of Berlin’s stamps became 4:5.
Cheryl had twice the total number of stamps that Andy and Berlin had.
How many stamps did Berlin and Cheryl have in total at first?
~~~~~~~~~~~~~~~~~~~~~~~~~
The solution and the answer in the post by @CPhill both are INCORRECT.
The best method to solve this problem is the BACKWARD method, and I will use it below.
I numbered the steps in the problem for easy references.
(a) Analyzing the ending situation from the problem
The stamps were circulated inside the team and did not go out or go into from outside.
Therefore, as they started with 6750 stamps at the beginning, so they ended with the same
6750 stamps at the end.
From it, we can analyze the ending situation from the problem.
The problem says that at the end
"Cheryl had twice the total number of stamps that Andy and Berlin had."
It means that at the end Cheryl had 2/3 of 6750, i.e. 4500 stamps, while Andy and Berlin
had 1/3 of 6750, or 2250 stamps, together.
Also, the problem says that at the end
"the ratio of the number of Andy’s stamps to the number of Berlin’s stamps became 4:5".
It means that at the end Andy had 4/9 of 2250, or 1000 stamps,
while Berlin had at the end 5/9 of 2250, or 1250 stamps.
So, at the end, Andy had 1000 stamps; Berlin had 1250 stamps, and Cheryl had 4500 stamps.
(b) Making steps back from the end to the beginning
(b32) From step (3) to step (2)
At step (3), Cheryl gave 1/6 of her stamps to Andy.
So, we can write this equation
C -  = 4500, or = 4500, or  = 4500, giving C = = 4500, giving C =  = 6*900 = 5400.
So, immediately before step (3), Cheryl had 5400 stamps.
Next, at step 3, Cheryl gave = 6*900 = 5400.
So, immediately before step (3), Cheryl had 5400 stamps.
Next, at step 3, Cheryl gave  = 900 stamps to Andy; so, immediately before step (3), Andy had 1000-900 = 100 stamps.
Thus, immediately after step 2, Andy had 100 stamps; Berlin had 1250 stamps; Cheryl had 5400 stamps.
(b21) From step (2) to step (1)
At step (2), Berlin gave 1/3 of her stamps to Cheryl.
So, we can write this equation
B - = 900 stamps to Andy; so, immediately before step (3), Andy had 1000-900 = 100 stamps.
Thus, immediately after step 2, Andy had 100 stamps; Berlin had 1250 stamps; Cheryl had 5400 stamps.
(b21) From step (2) to step (1)
At step (2), Berlin gave 1/3 of her stamps to Cheryl.
So, we can write this equation
B -  = 1250, or = 1250, or  = 1250, giving B = = 1250, giving B =  = 1875.
So, immediately before step (2), Berlin had 1875 stamps.
Next, at step 2, Berlin gave = 1875.
So, immediately before step (2), Berlin had 1875 stamps.
Next, at step 2, Berlin gave  = 625 stamps to Cheryl; so, immediately before step (2), Cheryl had 5400-625 = 4775 stamps.
Thus, immediately after step 1, Andy had 100 stamps; Berlin had 1875 stamps; Cheryl had 4775 stamps.
(b10) From step (1) to the beginning
At step (1), Andy gave 1/2 of his stamps to Berlin.
So, we can write this equation
A - = 625 stamps to Cheryl; so, immediately before step (2), Cheryl had 5400-625 = 4775 stamps.
Thus, immediately after step 1, Andy had 100 stamps; Berlin had 1875 stamps; Cheryl had 4775 stamps.
(b10) From step (1) to the beginning
At step (1), Andy gave 1/2 of his stamps to Berlin.
So, we can write this equation
A -  = 100, or = 100, or  = 100, giving A = 200.
So, at the beginning, Andy had 200 stamps.
Next, at step (1), Andy gave = 100, giving A = 200.
So, at the beginning, Andy had 200 stamps.
Next, at step (1), Andy gave  = 100 stamps to Berlin; so, at the beginning, Berlin had 1875-100 = 1775 stamps.
Thus, at the beginning, Andy had 200 stamps; Berlin had 1775 stamps, and Cheryl had 4775 stamps.
Finally, the problem asks "How many stamps did Berlin and Cheryl have in total at first ?"
The ANSWER is 1775 + 4775 = 6550. = 100 stamps to Berlin; so, at the beginning, Berlin had 1875-100 = 1775 stamps.
Thus, at the beginning, Andy had 200 stamps; Berlin had 1775 stamps, and Cheryl had 4775 stamps.
Finally, the problem asks "How many stamps did Berlin and Cheryl have in total at first ?"
The ANSWER is 1775 + 4775 = 6550.
Solved by the backward method.
I really think that this problem is INTENDED to be solved by the backward method
and that the backward method is the EXPECTED method on how this problem should be solved.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Andy, Berlin and Cheryl had a total of 6750 stamps. At first, Andy have 50% of his stamps to Berlin. Berlin then gave 1/3 of her
stamps to Cheryl. Finally, Cheryl gave 1/6 of her stamps to Andy. In the end, the ratio of the number of Andy’s stamps to the number
of Berlin’s stamps became 4:5. Cheryl had twice the total number of stamps that Andy and Berlin had. How many stamps did Berlin and
Cheryl have in total at first?
Whatever/Whomever it is that responded, is WRONG!!
Let initial amounts Andy, Berlin, and Cheryl had, be A, B, and C, respectively
A gave B 50% of his, so A’s remainder was .5A
B received 50% of A’s, or .5A, after which B had B + .5A
B, after giving  to C, had to C, had  left
C, after receiving left
C, after receiving  from B, then had: from B, then had:  C, after giving
C, after giving  to A, then had: to A, then had:  remaining
A, after receiving remaining
A, after receiving  of C’s, then had: of C’s, then had:  A:B = 4:5 ====>
A:B = 4:5 ====>  =====> =====>  =====>
=====>  =====>
=====>  =====>
=====>  4(6A + 12B) = 5(9.5A + B + 3C) ----- Cross-multiplying
24A + 48B = 47.5A + 5B + 15C
47.5A - 24A + 5B - 48B + 15C = 0
23.5A - 43B + 15C = 0 ---- eq (i)
Also, C = 2(A + B) ====> C = 2A + 2B ====> 2A + 2B - C = 0
4(6A + 12B) = 5(9.5A + B + 3C) ----- Cross-multiplying
24A + 48B = 47.5A + 5B + 15C
47.5A - 24A + 5B - 48B + 15C = 0
23.5A - 43B + 15C = 0 ---- eq (i)
Also, C = 2(A + B) ====> C = 2A + 2B ====> 2A + 2B - C = 0
 2(9.5A + B + 3C) + 6(2A + 4B) - (2.5A + 5B + 15C) = 0 ----- Multiplying by LCD, 18
19A + 2B + 6C + 12A + 24B - 2.5A - 5B - 15C = 0
19A + 12A - 2.5A + 2B + 24B - 5B + 6C - 15C = 0
28.5A + 21B - 9C = 0
2(9.5A + B + 3C) + 6(2A + 4B) - (2.5A + 5B + 15C) = 0 ----- Multiplying by LCD, 18
19A + 2B + 6C + 12A + 24B - 2.5A - 5B - 15C = 0
19A + 12A - 2.5A + 2B + 24B - 5B + 6C - 15C = 0
28.5A + 21B - 9C = 0
 ----- Dividing by 3
9.5A + 7B - 3C = 0 ----- eq (ii)
They ALL started with 6,750, so A + B + C = 6,750 ---- eq (iii)
23.5A - 43B + 15C = 0 ------- eq (i)
9.5A + 7B - 3C = 0 ------- eq (ii)
A + B + C = 6,750 --- eq (iii)
3A + 3B + 3C = 20,250 ---- Multiplying eq (iii) by 3 ---- eq (iv)
12.5A + 10B = 20,250 ---- Adding eqs (ii) & (iv) ----- Dividing by 3
9.5A + 7B - 3C = 0 ----- eq (ii)
They ALL started with 6,750, so A + B + C = 6,750 ---- eq (iii)
23.5A - 43B + 15C = 0 ------- eq (i)
9.5A + 7B - 3C = 0 ------- eq (ii)
A + B + C = 6,750 --- eq (iii)
3A + 3B + 3C = 20,250 ---- Multiplying eq (iii) by 3 ---- eq (iv)
12.5A + 10B = 20,250 ---- Adding eqs (ii) & (iv)
 ---- Dividing by 10
1.25A + B = 2,025
B = 2,025 - 1.25A ------ eq (v)
15A + 15B + 15C = 101,250 ----- Multiplying eq (iii) by 15 ---- eq (vi)
8.5A - 58B = - 101.250 --- Subtracting eq (vi) from eq (i) ---- eq (vii)
8.5A - 58(2,025 - 1.25A) = - 101,250 --- Substituting 2,025 - 1.25A for B in eq (vii)
8.5A - 117,450 + 72.5A = - 101,250
81A = - 101,250 + 117,450
81A = 16,200
Amount Andy had, initially, or A = ---- Dividing by 10
1.25A + B = 2,025
B = 2,025 - 1.25A ------ eq (v)
15A + 15B + 15C = 101,250 ----- Multiplying eq (iii) by 15 ---- eq (vi)
8.5A - 58B = - 101.250 --- Subtracting eq (vi) from eq (i) ---- eq (vii)
8.5A - 58(2,025 - 1.25A) = - 101,250 --- Substituting 2,025 - 1.25A for B in eq (vii)
8.5A - 117,450 + 72.5A = - 101,250
81A = - 101,250 + 117,450
81A = 16,200
Amount Andy had, initially, or A =  = 200
With ALL 3 starting with a total of 6,750 stamps, and A starting with 200, amount B and C started with = 6,750 - 200 = 6,550
You can do the CHECK!! = 200
With ALL 3 starting with a total of 6,750 stamps, and A starting with 200, amount B and C started with = 6,750 - 200 = 6,550
You can do the CHECK!!
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem step by step:
**Let's use variables:**
* A = Andy's initial number of stamps
* B = Berlin's initial number of stamps
* C = Cheryl's initial number of stamps
**1. Set up initial equation:**
* A + B + C = 6750
**2. Analyze the transactions step by step:**
* **Andy gives 50% to Berlin:**
* Andy now has A/2 stamps.
* Berlin now has B + A/2 stamps.
* **Berlin gives 1/3 to Cheryl:**
* Berlin now has (2/3)(B + A/2) = (2B + A)/3 stamps.
* Cheryl now has C + (B + A/2)/3 = (3C + B + A/2)/3 stamps.
* **Cheryl gives 1/6 to Andy:**
* Cheryl now has (5/6)(3C + B + A/2)/3 = (15C + 5B + 5A/2)/18 stamps.
* Andy now has A/2 + (3C + B + A/2)/18 = (9A + 3C + B)/18 + A/2 = (9A + 3C + B + 9A)/18 = (18A + 3C + B)/18 stamps
**3. Set up equations based on the final amounts:**
* **Ratio of Andy's to Berlin's stamps:**
(18A + 3C + B)/18 : (2B + A)/3 = 4 : 5
Simplifying gives: 5(18A + 3C + B) = 24(2B+A)
90A + 15C + 5B = 48B + 24A
66A - 43B + 15C = 0
* **Cheryl has twice the total of Andy and Berlin:**
(15C + 5B + 5A/2)/18 = 2 * [(18A + 3C + B)/18 + (2B+A)/3]
15C + 5B + 5A/2 = 2 * [18A + 3C + B + 6(2B+A)]
15C + 5B + 5A/2 = 2 * [18A + 3C + B + 12B + 6A]
15C + 5B + 5A/2 = 2 * [24A + 3C + 13B]
15C + 5B + 5A/2 = 48A + 6C + 26B
9C - 21B - 91A/2=0
18C - 42B - 91A = 0
**4. Solve the system of equations:**
We have three equations:
1. A + B + C = 6750
2. 66A - 43B + 15C = 0
3. 18C - 42B - 91A = 0
Solving this system of equations (using substitution or elimination) is a bit involved, but it will lead to the solutions: A = 1500, B = 2000, and C = 3250.
**5. Find the total for Berlin and Cheryl initially:**
B + C = 2000 + 3250 = 5250
**Answer:** Berlin and Cheryl had a total of 5250 stamps at first.
Question 1209742: Ayodeji was 1.5m tall when he took a snapshot of himself. If the scale factor of the picture is 1:10, what is his height in the photograph
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find Ayodeji's height in the photograph, we need to multiply his actual height by the scale factor.
* **Ayodeji's actual height:** 1.5 meters
* **Scale factor:** 1:10 (which means 1/10)
Height in photograph = Actual height * Scale factor
Height in photograph = 1.5 meters * (1/10)
Height in photograph = 0.15 meters
Therefore, Ayodeji's height in the photograph is 0.15 meters.
Question 1209703: Brad uses 1/8 of a cup of vinegar in his salad dressing recipe. How much vinegar would Brad use to make 1/3 of a recipe?
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1209584: 40% of Alan's marbles is equal to 50% of what Bryan has. They both have 540 marbles altogether. How many marbles must Alan give to Bryan so that they each have the same number of marbles
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
40% of Alan's marbles is equal to 50% of what Bryan has.
They both have 540 marbles altogether.
How many marbles must Alan give to Bryan so that they each have the same number of marbles
~~~~~~~~~~~~~~~~~~~~
Below is my mental solution.
The statement
"40% of Alan's marbles is equal to 50% of what Bryan has"
is equivalent to
"80% of Alan's marbles is equal to 100% of what Bryan has."
+---------------------------------------------------------------+
| Or, in other words, |
| for each 20 marbles that Bryan has, Alan has 25 marbles. |
+---------------------------------------------------------------+
It means that we can group their marbles evenly in sets (25 Alan's marbles, 20 Bryan's marbles).
Each such a set has 25+20 = 45 marbles; so, the number of all such sets is 540/45 = 12.
So, Alan has 25*12 = 300 marbles; Bryan has 20*12 = 240 marbles.
Thus, Alan should give half of the difference, 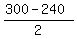 = 30 marbles to Brian
to equate the numbers of their marbles. = 30 marbles to Brian
to equate the numbers of their marbles.
Solved.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1186153: In a limited environment where A is the maximum number of bacteria supportable by the environment, the rate of bacterial growth is directly proportional to the number present and the difference between A and the number present. Suppose 1 million bacteria is the maximum number supportable by the environment and the rate of growth is 60 bacteria per minute when there are 1000 bacteria present.
Find the rate of growth when there are 100,000 bacteria present.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
**1. Set up the differential equation:**
Let *B(t)* be the number of bacteria at time *t*. The problem states that the rate of growth is directly proportional to the number present and the difference between A and the number present. This can be written as:
dB/dt = k * B * (A - B)
where *k* is the proportionality constant.
**2. Use the given information to find *k*:**
We know that A = 1,000,000, and when B = 1000, dB/dt = 60. Plugging these values into the equation:
60 = k * 1000 * (1,000,000 - 1000)
60 = k * 1000 * 999,000
k = 60 / (1000 * 999,000)
k = 6 / 999,000
k ≈ 6.006 x 10⁻⁸
**3. Find the rate of growth when B = 100,000:**
Now we want to find dB/dt when B = 100,000. Using the same equation and the calculated value of *k*:
dB/dt = (6.006 x 10⁻⁸) * 100,000 * (1,000,000 - 100,000)
dB/dt = (6.006 x 10⁻⁸) * 100,000 * 900,000
dB/dt = 5405.4 bacteria per minute
**Answer:**
The rate of growth when there are 100,000 bacteria present is approximately 5405.4 bacteria per minute.
Question 1186579: Good evening! I sure wish there was a way to submit images on here. I have such a headache trying to figure this out and I really want to understand.
So this problem shows an image of two hexagons stacked. The top hexagon has three triangles kind of like a crown on top. This is what it says: The area of Design B is 5/3 of the area of another design. Make a design that could be the other design. Explain your reasoning.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to approach this problem:
**Understanding the Relationship**
Design B's area is 5/3 *larger* than the area of the unknown design (let's call it Design A). This means Design A is *smaller* than Design B. To find Design A, we need to find a shape whose area is 3/5 of Design B's area.
**Analyzing Design B**
Let's break down Design B into simpler shapes to make calculating its area easier. We can see Design B is composed of:
* Two regular hexagons (one on top of the other)
* Three equilateral triangles
**Making Design A**
The key is to create a design that is visually and proportionally similar to Design B but smaller. Since the area of Design B can be expressed as 5/3 of the area of Design A, Design A will have 3/5 the area of Design B. Here's one way to do it:
1. **Start with one hexagon:** Take *one* of the hexagons from Design B. This will be the base of Design A.
2. **Add proportionally smaller triangles:** The three triangles on top of Design B are equilateral. We need to create three *smaller* equilateral triangles for Design A. A good approach is to make each side of the new equilateral triangle equal to one half the side of the original triangles. In this way, the area of the new triangles is 1/4 of the area of the original triangles.
**Reasoning**
* **Hexagon:** By using only *one* hexagon instead of two, we've reduced the hexagonal area by half.
* **Triangles:** Because the area of a triangle is proportional to the square of its side length, halving the side length makes the area one-quarter of the original triangle. Since Design B has three triangles, Design A will have three triangles each with 1/4 the area of the triangles in design B.
**Why this works (Area Calculation)**
Let 'h' be the area of one hexagon, and 't' be the area of one triangle in Design B. The area of Design B = 2h + 3t.
Design A contains one hexagon and three triangles. The area of the hexagon is h. The area of each triangle is t/4. The area of the three triangles will be 3t/4. The total area of Design A will be h + 3t/4.
If we take the ratio of Design B to Design A we get (2h + 3t)/(h + 3t/4) = 5/3.
**Visual Representation**
It's best to draw this out. Design B looks like two hexagons stacked with a "crown" of three triangles. Design A would look like *one* hexagon with a smaller "crown" of three smaller triangles on top.
This method creates a Design A that is proportionally similar to Design B and has the correct area relationship (3/5 of Design B's area).
Question 1189268: Dr. de Campo was listing systolic blood pressure data for a group of her patients. The numbers were 126,101,99,111,101,105,142,126, and 124. Justin's blood pressure was 124 on the list. What was his deviation score?
Answer (to the nearest hundredths)
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate Justin's deviation score:
1. **Calculate the mean of the blood pressure data:**
(126 + 101 + 99 + 111 + 101 + 105 + 142 + 126 + 124) / 9 = 117.22
2. **Subtract the mean from Justin's blood pressure:**
124 - 117.22 = 6.78
**Answer:** Justin's deviation score is 6.78.
Question 1190543: In each of the following parts, the people named shared all of a large candy bar. Make a drawing and give your reasoning in finding what fraction of the bar each person ate. a) Tome ate 2/3 as much as Ulysses ate. b) Vicky ate 3/4 as much as Willie, who ate half as much as Xavier. e) Yolanda ate 1/3 of the bar, Zeb ate 3/4 of what Yolanda left, and then Arnie ate the rest.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Tome and Ulysses**
* **Drawing:** Imagine the candy bar divided into 5 equal pieces. Ulysses eats 3 of those pieces, and Tome eats 2.
* **Reasoning:** Since Tome ate 2/3 as much as Ulysses, we can represent their shares as a ratio of 2:3. This means the candy bar needs to be divided into 2 + 3 = 5 equal parts.
* **Fractions:** Ulysses ate 3/5 of the candy bar, and Tome ate 2/5 of the candy bar.
**b) Vicky, Willie, and Xavier**
* **Drawing:** Picture the candy bar divided into 8 equal pieces. Xavier eats 4 pieces, Willie eats 2 pieces, and Vicky eats 1.5 pieces (imagine splitting one piece in half).
* **Reasoning:** We're given that Willie ate half as much as Xavier. Let's say Xavier ate 4 pieces (it's easiest to work with whole numbers). This means Willie ate 4 / 2 = 2 pieces. Vicky ate 3/4 as much as Willie, so she ate (3/4) * 2 = 1.5 pieces. In total, they ate 4 + 2 + 1.5 = 7.5 pieces. To make this work with fractions, we can double the number of pieces to 16. Now Xavier has 8, Willie has 4, and Vicky has 3.
* **Fractions:** Xavier ate 8/16 (or 1/2) of the candy bar, Willie ate 4/16 (or 1/4) of the candy bar, and Vicky ate 3/16 of the candy bar.
**c) Yolanda, Zeb, and Arnie**
* **Drawing:** Divide the candy bar into thirds. Yolanda eats one-third. Then divide the remaining two-thirds into quarters. Zeb eats three of those quarters. The remaining quarter is for Arnie.
* **Reasoning:** Yolanda ate 1/3 of the bar, leaving 1 - 1/3 = 2/3 remaining. Zeb ate 3/4 of the remaining portion, so he ate (3/4) * (2/3) = 1/2 of the whole candy bar. Arnie ate the rest, which is 1 - 1/3 - 1/2 = 1/6 of the candy bar.
* **Fractions:** Yolanda ate 1/3 of the candy bar, Zeb ate 1/2 of the candy bar, and Arnie ate 1/6 of the candy bar.
Question 1191224: The current ratio of Precision Machine. Products is 3.8. If
the firm’s current assets are $570,000, what are its current
liabilities? To raise additional funds, what is the maximum
amount the company can borrow on a short-term basis if
the current ratio is to be no less than 2.6?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
**1. Calculate Current Liabilities:**
* Current Ratio = Current Assets / Current Liabilities
* 3.8 = $570,000 / Current Liabilities
* Current Liabilities = $570,000 / 3.8
* Current Liabilities = $150,000
**2. Calculate the Maximum Borrowing Amount:**
* We want the current ratio to be no less than 2.6 after borrowing. Let 'x' be the amount borrowed.
* New Current Assets = $570,000 + x
* New Current Liabilities = $150,000 + x
* New Current Ratio = (New Current Assets) / (New Current Liabilities)
* 2.6 = ($570,000 + x) / ($150,000 + x)
Now, solve for x:
* 2.6 * ($150,000 + x) = $570,000 + x
* $390,000 + 2.6x = $570,000 + x
* 1.6x = $180,000
* x = $112,500
Therefore, the maximum amount the company can borrow on a short-term basis is $112,500.
Question 1205101: Let’s say you are buying protein bars for your gym. You have a total of x protein bars. If 10% of the bars are chocolate flavor, 20% are peanut butter flavor, and half of the remaining bars are vanilla flavor, and you have 420 bars in total, how many protein bars do you have in total?
Found 3 solutions by ikleyn, greenestamps, ArschlochGeometrie:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Somewhere half-way between a stupid joke, nonsense and an attempt to confuse a reader.
A typical bad style puzzle, of the lowest possible level.
It is clear that the author suffers from idleness. My condolences.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by ArschlochGeometrie(3)  (Show Source): (Show Source):
Question 1209350: Rama was getting some items for the new school year. First, he bought some textbooks with $8 more than 1/3 of his money. Next, Next, he bought his stationery with $12.20 less than 1/2 of his remaining money. Lastly, he bought some school socks with $2.80 more than 1/2 of the money left. Then, he had $15.40 with him. How much money did he have at first?
Found 4 solutions by MathTherapy, greenestamps, mccravyedwin, proyaop:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Looks like AI got this one correct. AI will get better and better, but you
can't trust it with everything yet. There is still some use for us humans.
So I'll do it the human way.
------------
Rama was getting some items for the new school year.
Let x = the amount at first.
First, he bought some textbooks with $8 more than 1/3 of his money.
Let y = how much he had left after buying textbooks.


 Next, he bought his stationery with $12.20 less than 1/2 of his remaining money.
Let z = how much he had left after buying stationery.
Next, he bought his stationery with $12.20 less than 1/2 of his remaining money.
Let z = how much he had left after buying stationery.


 Lastly, he bought some school socks with $2.80 more than 1/2 of the money left.
Let w = how much he had left after buying socks.
Lastly, he bought some school socks with $2.80 more than 1/2 of the money left.
Let w = how much he had left after buying socks.


 Then, he had $15.40 with him.
Then, he had $15.40 with him.

 How much money did he have at first?
Substitute the 4th equation in the 3rd equation
How much money did he have at first?
Substitute the 4th equation in the 3rd equation


 Substitute that in the 2nd equation
Substitute that in the 2nd equation


 Substitute that in the 1st equation
Substitute that in the 1st equation



 Answer: $84.60 <--SOLUTION!
Checking:
He had $84.60
First, he bought some textbooks with $8 more than 1/3 of his money.
1/3 of his 84.60 or 28.20, plus 8 is 36.20, which was what he spent,
so he had 84.60-36.20 or 48.40 left.
Next, he bought his stationery with $12.20 less than 1/2 of his remaining money.
1/2 of his remaining money was 1/2 of 48.40, or 24.20, minus 12.20, or 12,
which was what he spent, so he had 48.40-12 or 36.40 left.
Lastly, he bought some school socks with $2.80 more than 1/2 of the money left.
1/2 of his remaining money was 1/2 of 36.40, or 18.20, plus 2.80, or 21,
which was what he spent, so he had 36.40-21 or 15.40 left.
Then, he had $15.40 with him.
So now we know we have the right answer, $84.60.
Edwin
Answer: $84.60 <--SOLUTION!
Checking:
He had $84.60
First, he bought some textbooks with $8 more than 1/3 of his money.
1/3 of his 84.60 or 28.20, plus 8 is 36.20, which was what he spent,
so he had 84.60-36.20 or 48.40 left.
Next, he bought his stationery with $12.20 less than 1/2 of his remaining money.
1/2 of his remaining money was 1/2 of 48.40, or 24.20, minus 12.20, or 12,
which was what he spent, so he had 48.40-12 or 36.40 left.
Lastly, he bought some school socks with $2.80 more than 1/2 of the money left.
1/2 of his remaining money was 1/2 of 36.40, or 18.20, plus 2.80, or 21,
which was what he spent, so he had 36.40-21 or 15.40 left.
Then, he had $15.40 with him.
So now we know we have the right answer, $84.60.
Edwin
Answer by proyaop(69)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Let's represent:**
* The initial amount of money Rama had as 'x'
**2. Formulate the equation:**
* **Textbooks:** Rama spent (x/3) + 8 dollars on textbooks.
* **Remaining money after textbooks:** x - (x/3) - 8 = (2/3)x - 8
* **Stationery:** Rama spent 1/2 * ((2/3)x - 8) - 12.20 dollars on stationery.
* **Remaining money after stationery:** (2/3)x - 8 - 1/2 * ((2/3)x - 8) + 12.20 = (2/3)x - 8 - (1/3)x + 4 + 12.20 = (1/3)x + 8.20
* **School Socks:** Rama spent 1/2 * ((1/3)x + 8.20) + 2.80 dollars on socks.
* **Remaining money:** (1/3)x + 8.20 - 1/2 * ((1/3)x + 8.20) - 2.80 = 15.40
**3. Simplify and solve the equation:**
* (1/3)x + 8.20 - (1/6)x - 4.10 - 2.80 = 15.40
* (1/6)x + 1.30 = 15.40
* (1/6)x = 14.10
* x = 14.10 * 6
* x = 84.60
**Therefore, Rama had $84.60 at first.**
Question 1193539: (1) The weight of cement bags produced in a cement company follow normal distribution
whose population is infinite. The expected mean of weight of the cement bags for sales of
this population is 45KG and its variance is unknown. The sales manager of the firm
claims that the mean weight of the cement bags is significantly more than the expected
mean weight of the population. So, he has selected a random sample of 36 bags and its
mean and variance are found to be 44KG and 1.25KG, respectively. Verify the intuition
of the sales manager at a significance level of 0.05.
(2) The quality manager of a washing machine company feels that the mean time between
failures of the motors received is at most 90 days. The quality manager wants to test his
intuition. Hence, he has taken a sample of 25 motors whose mean time between failure
and its variance are found to be 93 days and 16 days, respectively. Verify the intuition of
the quality manager at a significance level of 0.05.
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's analyze both scenarios.
**1. Cement Bag Weights**
**a) Set up Hypotheses**
* **Null Hypothesis (H0):** The mean weight of the cement bags is less than or equal to the expected mean weight.
* μ ≤ 45 kg
* **Alternative Hypothesis (H1):** The mean weight of the cement bags is significantly greater than the expected mean weight.
* μ > 45 kg
**b) Choose the Test Statistic**
* Since the population variance is unknown and the sample size is greater than 30, we can use the **one-sample t-test**.
**c) Calculate the Test Statistic**
* **Given:**
* Sample size (n): 36
* Sample mean (x̄): 44 kg
* Sample variance (s²): 1.25 kg²
* Population mean (μ₀): 45 kg
* **Calculate the standard error:**
* Standard Error (SE) = s / √n
* SE = √(1.25) / √36
* SE ≈ 0.2041
* **Calculate the t-score:**
* t = (x̄ - μ₀) / SE
* t = (44 - 45) / 0.2041
* t ≈ -4.898
**d) Determine Critical Value**
* **Significance Level:** α = 0.05
* **Degrees of Freedom (df):** n - 1 = 36 - 1 = 35
* **One-tailed test (right-tailed):** Find the critical t-value from a t-distribution table.
* t_critical ≈ 1.690
**e) Decision Rule**
* If the calculated t-score is greater than the critical t-value, reject the null hypothesis.
* If the calculated t-score is less than or equal to the critical t-value, fail to reject the null hypothesis.
**f) Make a Decision**
* Our calculated t-score (-4.898) is less than the critical t-value (1.690).
* **Conclusion:** We fail to reject the null hypothesis.
**Interpretation**
The evidence does not support the sales manager's claim that the mean weight of the cement bags is significantly greater than the expected mean weight.
**2. Washing Machine Motor Time Between Failures**
**a) Set up Hypotheses**
* **Null Hypothesis (H0):** The mean time between failures is less than or equal to 90 days.
* μ ≤ 90 days
* **Alternative Hypothesis (H1):** The mean time between failures is greater than 90 days.
* μ > 90 days
**b) Choose the Test Statistic**
* Similar to the first scenario, we can use the **one-sample t-test** since the population variance is unknown.
**c) Calculate the Test Statistic**
* **Given:**
* Sample size (n): 25
* Sample mean (x̄): 93 days
* Sample variance (s²): 16 days²
* Population mean (μ₀): 90 days
* **Calculate the standard error:**
* SE = s / √n
* SE = √(16) / √25
* SE = 4 / 5
* SE = 0.8 days
* **Calculate the t-score:**
* t = (x̄ - μ₀) / SE
* t = (93 - 90) / 0.8
* t = 3 / 0.8
* t = 3.75
**d) Determine Critical Value**
* **Significance Level:** α = 0.05
* **Degrees of Freedom (df):** n - 1 = 25 - 1 = 24
* **One-tailed test (right-tailed):** Find the critical t-value from a t-distribution table.
* t_critical ≈ 1.711
**e) Decision Rule**
* If the calculated t-score is greater than the critical t-value, reject the null hypothesis.
* If the calculated t-score is less than or equal to the critical t-value, fail to reject the null hypothesis.
**f) Make a Decision**
* Our calculated t-score (3.75) is greater than the critical t-value (1.711).
* **Conclusion:** We reject the null hypothesis.
**Interpretation**
The evidence supports the quality manager's intuition that the mean time between failures of the motors is significantly greater than 90 days.
Question 1193540: (a) The regional manager of a bank wants to analyze the number of delayed repayments of
instalments of consumer loans in two of its branch banks (Branch −X and Branch −Y ).
The number of delayed payments of instalments in each branch bank follows normal
distribution. The manager feels that the number of delayed payments of instalments by
the consumers of the Branch −X is no way different from that of the Branch −Y . So, he
selected the loan accounts of 80 different consumers from the Branch −X and found that
the mean and variance of the number of delayed payments of instalments are 35 and 25,
respectively. Similarly, he selected the loan accounts of 100 different consumers from the Branch −Y and found that the mean and variance of the number of delayed payments of
instalments are 40 and 49, respectively. Test his intuition at a significance level of 0.01.
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Set up Hypotheses**
* **Null Hypothesis (H0):** The mean number of delayed payments of installments is the same for both branches.
* μ₁ = μ₂
* **Alternative Hypothesis (H1):** The mean number of delayed payments of installments is different for the two branches.
* μ₁ ≠ μ₂
**2. Choose the Test Statistic**
* Since we are comparing the means of two independent samples with known (or assumed) population variances, we will use the **Z-test for the difference between two means**.
**3. Calculate the Test Statistic**
* **Given:**
* Sample 1 (Branch X): n₁ = 80, x̄₁ = 35, σ₁² = 25
* Sample 2 (Branch Y): n₂ = 100, x̄₂ = 40, σ₂² = 49
* **Calculate the pooled variance (not needed in this case since population variances are known):**
* Pooled variance (s_p²) = [(n₁ - 1)s₁² + (n₂ - 1)s₂²] / (n₁ + n₂ - 2)
* **Calculate the standard error of the difference between means:**
* SE = √[(σ₁²/n₁) + (σ₂²/n₂)]
* SE = √[(25/80) + (49/100)]
* SE = √(0.3125 + 0.49)
* SE = √0.8025
* SE ≈ 0.8958
* **Calculate the Z-score:**
* Z = (x̄₁ - x̄₂) / SE
* Z = (35 - 40) / 0.8958
* Z = -5 / 0.8958
* Z ≈ -5.58
**4. Determine Critical Values**
* **Significance Level:** α = 0.01
* **Two-tailed test:** We need to find the critical values for both tails of the standard normal distribution.
* **Using a standard normal distribution table or statistical software:**
* Critical values: Z_critical ≈ ±2.576
**5. Decision Rule**
* If the calculated Z-score (|Z|) is greater than the critical value (Z_critical), reject the null hypothesis.
* If the calculated Z-score (|Z|) is less than or equal to the critical value (Z_critical), fail to reject the null hypothesis.
**6. Make a Decision**
* Our calculated Z-score (|-5.58|) is greater than the critical value (2.576).
* **Conclusion:** We reject the null hypothesis.
**Interpretation**
The evidence suggests that the mean number of delayed payments of installments is significantly different between Branch X and Branch Y at the 0.01 significance level.
**Therefore, the manager's intuition that the number of delayed payments is the same for both branches is not supported by the data.**
Question 1193541: The weight of a drug produced by a pharmaceutical company follows normal
distribution. The specified variances of the weight of the drug of this population is
0.36KG. The quality engineer of the firm claims that the variance of the weight of the
drug does not differ significantly from the specified variance of the weight of the drug of
the population. So, the purchase manager of a hospital who places order for the drug with
the pharmaceutical company has selected a random sample of 15 drugs. The variance of
the weight of the sample is found to be 0.05KG. Verify the intuition of the quality
engineer of the pharmaceutical company at a significance level of 0.05.
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Set up Hypotheses**
* **Null Hypothesis (H0):** The variance of the drug weight in the sample is equal to the specified population variance.
* σ² = 0.36 kg²
* **Alternative Hypothesis (H1):** The variance of the drug weight in the sample is different from the specified population variance.
* σ² ≠ 0.36 kg²
**2. Test Statistic**
* We will use the chi-square test statistic for this hypothesis test:
χ² = (n - 1) * s² / σ²
where:
* n is the sample size (15)
* s² is the sample variance (0.05 kg²)
* σ² is the population variance (0.36 kg²)
**3. Calculate Test Statistic**
χ² = (15 - 1) * 0.05 / 0.36
χ² = 14 * 0.05 / 0.36
χ² ≈ 1.94
**4. Determine Critical Values**
* **Degrees of Freedom:** df = n - 1 = 15 - 1 = 14
* **Significance Level:** α = 0.05
* **Two-tailed test:** We need to find the critical values for both tails of the chi-square distribution.
* **Find critical values using a chi-square table or statistical software:**
* Lower critical value (χ²_lower) ≈ 5.629
* Upper critical value (χ²_upper) ≈ 26.119
**5. Decision Rule**
* If the calculated chi-square statistic (χ²) falls within the critical region (below χ²_lower or above χ²_upper), we reject the null hypothesis.
* If the calculated chi-square statistic falls within the acceptance region (between χ²_lower and χ²_upper), we fail to reject the null hypothesis.
**6. Make a Decision**
* Our calculated χ² (1.94) is less than the lower critical value (5.629).
* **Conclusion:** We reject the null hypothesis.
**Interpretation**
The evidence suggests that the variance of the drug weight in the sample is significantly different from the specified population variance at the 0.05 significance level.
**Therefore, the quality engineer's claim that the variance of the drug weight does not differ significantly from the specified variance is not supported by the sample data.**
Question 1193544: The random variable X has a probability distribution
x. 1 2 3 4 5
P X x ( = ) 0.1 p q 0.3 0.1
i. Given that E X( ) = 3.1, write down two equations involving p and q .
ii. Find the values of p and q .
iii. Find Var X( )
iv. Var X (2 3 .
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! **i. Find two equations involving p and q:**
1. **Sum of Probabilities:**
The sum of all probabilities in a probability distribution must equal 1.
Therefore: 0.1 + p + q + 0.3 + 0.1 = 1
Simplifying: p + q = 0.5
2. **Expected Value (E(X)):**
E(X) = Σ [x * P(X = x)]
Given E(X) = 3.1, we have:
3.1 = (1 * 0.1) + (2 * p) + (3 * q) + (4 * 0.3) + (5 * 0.1)
3.1 = 0.1 + 2p + 3q + 1.2 + 0.5
3.1 = 1.8 + 2p + 3q
Simplifying: 2p + 3q = 1.3
**ii. Find the values of p and q:**
* We have two equations:
* p + q = 0.5
* 2p + 3q = 1.3
* Solve this system of equations:
* From the first equation, isolate p: p = 0.5 - q
* Substitute this value of p into the second equation:
2(0.5 - q) + 3q = 1.3
1 - 2q + 3q = 1.3
q = 0.3
* Substitute the value of q back into the first equation:
p + 0.3 = 0.5
p = 0.2
* Therefore, p = 0.2 and q = 0.3
**iii. Find Var(X)**
* **Calculate E(X²)**:
E(X²) = Σ [x² * P(X = x)]
E(X²) = (1² * 0.1) + (2² * 0.2) + (3² * 0.3) + (4² * 0.3) + (5² * 0.1)
E(X²) = 0.1 + 0.8 + 2.7 + 4.8 + 2.5
E(X²) = 10.9
* **Calculate Var(X)**:
Var(X) = E(X²) - [E(X)]²
Var(X) = 10.9 - (3.1)²
Var(X) = 10.9 - 9.61
Var(X) = 1.29
**iv. Find Var(2X - 3)**
* Use the property: Var(aX + b) = a² * Var(X)
where a = 2 and b = -3
* Var(2X - 3) = 2² * Var(X)
Var(2X - 3) = 4 * 1.29
Var(2X - 3) = 5.16
**Summary:**
* p = 0.2
* q = 0.3
* Var(X) = 1.29
* Var(2X - 3) = 5.16
Question 1195642: A Une poutre horizontale uniforme mesure 20 pieds de long et pèse 400 livres. Il est supporté par deux colonnes A et B représentées. Une charge verticale de 1 200 lb est appliquée à la poutre à la distance x de la colonne B (comme illustré). Trouvez x distance si la réaction à la colonne A est de 500 livres.
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! ## Compréhension du Problème et Diagramme
**Problème:**
On a une poutre horizontale de 20 pieds, chargée de 400 lb (son propre poids) et d'une charge supplémentaire de 1200 lb à une distance x de la colonne B. On cherche à déterminer la valeur de x sachant que la réaction à la colonne A est de 500 lb.
**Diagramme:**
[Image d'une poutre horizontale de 20 pieds avec les colonnes A et B à chaque extrémité. Une charge de 400 lb est répartie uniformément sur la poutre. Une charge de 1200 lb est appliquée à une distance x de B. Les réactions en A et B sont indiquées.]
## Résolution du Problème
**Principe Fondamental de la Statique:**
Pour un corps en équilibre, la somme des forces verticales et la somme des moments doivent être nulles.
**Équations d'équilibre:**
1. **Somme des forces verticales = 0:**
* RA + RB - 400 lb - 1200 lb = 0
* On sait que RA = 500 lb, donc :
* 500 lb + RB - 1600 lb = 0
* RB = 1100 lb
2. **Somme des moments autour du point A = 0:**
* Prenons les moments dans le sens antihoraire comme positifs.
* (400 lb * 10 ft) + (1200 lb * x) - (1100 lb * 20 ft) = 0
* 4000 ft.lb + 1200x ft.lb - 22000 ft.lb = 0
* 1200x = 18000 ft.lb
* x = 15 ft
## Conclusion
**La distance x de la charge de 1200 lb à la colonne B est de 15 pieds.**
**En résumé:**
Pour trouver la distance x, nous avons utilisé les deux équations d'équilibre de la statique : la somme des forces verticales est nulle et la somme des moments autour d'un point est nulle. En résolvant ces équations, nous avons pu déterminer la valeur de x.
**Remarque:**
Ce type de problème est couramment rencontré en statique et en résistance des matériaux. Il est important de bien comprendre les principes fondamentaux de la statique pour résoudre ce genre d'exercices.
**Avez-vous d'autres questions sur ce problème ou souhaitez-vous aborder un autre exercice ?**
Question 1196639: A relief organization must track their supply and demand for various blood types. They estimate that about 46% of the population in a country has Type O blood, 42% Type A, 9% Type B, and the rest Type AB.
a) If someone volunteers to give blood, what is the probability that this donor: i) Has Type AB blood? ii) Has Type A or Type B blood? iii) Is not Type O?
b) Among four potential donors, what is the probability that: i) All are Type O? ii) None have Type AB blood? iii) Not all are Type A? iv) At least one person is Type B?
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Probabilities for a Single Donor**
* **i) Has Type AB blood:**
* Probability = 100% - (46% + 42% + 9%) = 3%
* **ii) Has Type A or Type B blood:**
* Probability = 42% + 9% = 51%
* **iii) Is not Type O blood:**
* Probability = 100% - 46% = 54%
**b) Probabilities for Four Donors**
* **i) All are Type O:**
* Probability = (0.46) * (0.46) * (0.46) * (0.46) = 0.46^4 ≈ 0.0457 (or 4.57%)
* **ii) None have Type AB blood:**
* Probability of not having Type AB = 100% - 3% = 97%
* Probability that none have Type AB = (0.97) * (0.97) * (0.97) * (0.97) = 0.97^4 ≈ 0.8853 (or 88.53%)
* **iii) Not all are Type A:**
* Probability that all are Type A = (0.42) * (0.42) * (0.42) * (0.42) = 0.42^4 ≈ 0.0311 (or 3.11%)
* Probability that not all are Type A = 100% - 3.11% = 96.89%
* **iv) At least one person is Type B:**
* Probability that none are Type B = (1 - 0.09)^4 = 0.6860
* Probability that at least one person is Type B = 100% - 68.60% = 31.40%
**Note:** These calculations assume that the blood types of the donors are independent of each other.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050
|
| |






