Question 945242: P(-1,-2), Q(5,k), R(8,2), S(h,1) are the four vertices of the parallelogram PQRS, Find the value of h, and the value of k.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
given:
P( , , ), Q( ), Q( , , ), R( ), R( , , ), S( ), S( , , ) are the four vertices of the parallelogram ) are the four vertices of the parallelogram  , ,
the parallelogram is quadrilateral with two pairs of 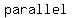 and and  in length sides in length sides
 is parallel and equal to is parallel and equal to 
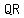 is parallel and equal to is parallel and equal to 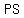
distance from  and and  is equal to distance from is equal to distance from  to to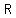
and
distance from  and and  is equal to distance from is equal to distance from  to to 
Now use the distance formula to find the distance between the two points, P( , , ) and Q( ) and Q( , , ): ):



 => this is also equal to distance from R( => this is also equal to distance from R( , , ) to S( ) to S( , , ) )




since  is parallel and equal to is parallel and equal to  , we have , we have
 ......square both sides ......square both sides

 ........eq.1 ........eq.1
now find the distance between the two other points Q( , , ) and R( ) and R( , , ) )




then, between the two other points P( , , ) and S( ) and S( , , ) )




so,

 ........eq.2 ........eq.2
solve the system:
 ........eq.1 ........eq.1
 ........eq.2 ........eq.2
-------------------------------------------subtract 2 from 1


 ...solve for ...solve for 


 .............substitute in eq.1 .............substitute in eq.1
 ........eq.1 ...solve for ........eq.1 ...solve for 

 .......use quadratic formula .......use quadratic formula




 or or 
we will use  and find and find 



so, we will have points:
P( , , ), Q( ), Q( , , ), R( ), R( , , ), S( ), S( , , ) )
now we can graph a parallelogram 

|
|
|